Linear continuum

Last updated April 07, 2023

In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line.

Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two distinct elements there is another (and hence infinitely many others), and complete, i.e., which "lacks gaps" in the sense that every nonempty subset with an upper bound has a least upper bound. More symbolically:

S has the least upper bound property, and
For each x in S and each y in S with x < y, there exists z in S such that x < z < y

A set has the least upper bound property, if every nonempty subset of the set that is bounded above has a least upper bound in the set. Linear continua are particularly important in the field of topology where they can be used to verify whether an ordered set given the order topology is connected or not.^[1]

Unlike the standard real line, a linear continuum may be bounded on either side: for example, any (real) closed interval is a linear continuum.

Examples

The ordered set of real numbers, R, with its usual order is a linear continuum, and is the archetypal example. Property b) is trivial, and property a) is simply a reformulation of the completeness axiom.

Examples in addition to the real numbers:

sets which are order-isomorphic to the set of real numbers, for example a real open interval, and the same with half-open gaps (note that these are not gaps in the above-mentioned sense)
the affinely extended real number system and order-isomorphic sets, for example the unit interval
the set of real numbers with only +∞ or only −∞ added, and order-isomorphic sets, for example a half-open interval
the long line
The set I × I (where × denotes the Cartesian product and I = [0, 1]) in the lexicographic order is a linear continuum. Property b) is trivial. To check property a), we define a map, π₁ : I × I → I by

π₁ (x, y) = x

This map is known as the projection map. The projection map is continuous (with respect to the product topology on I × I) and is surjective. Let A be a nonempty subset of I × I which is bounded above. Consider π₁(A). Since A is bounded above, π₁(A) must also be bounded above. Since, π₁(A) is a subset of I, it must have a least upper bound (since I has the least upper bound property). Therefore, we may let b be the least upper bound of π₁(A). If b belongs to π₁(A), then b × I will intersect A at say b × c for some c ∈ I. Notice that since b × I has the same order type of I, the set (b × I) ∩ A will indeed have a least upper bound b × c', which is the desired least upper bound for A.

If b does not belong to π₁(A), then b × 0 is the least upper bound of A, for if d < b, and d × e is an upper bound of A, then d would be a smaller upper bound of π₁(A) than b, contradicting the unique property of b.

Non-examples

The ordered set Q of rational numbers is not a linear continuum. Even though property b) is satisfied, property a) is not. Consider the subset

A = {x ∈ Q | x < √2}

of the set of rational numbers. Even though this set is bounded above by any rational number greater than √2 (for instance 3), it has no least upper bound in the rational numbers.^[2] (Specifically, for any rational upper bound r > √2, r/2 + 1/r is a closer rational upper bound; details at Methods of computing square roots § Heron's method.)

The ordered set of non-negative integers with its usual order is not a linear continuum. Property a) is satisfied (let A be a subset of the set of non-negative integers that is bounded above. Then A is finite so it has a maximum, and this maximum is the desired least upper bound of A). On the other hand, property b) is not. Indeed, 5 is a non-negative integer and so is 6, but there exists no non-negative integer that lies strictly between them.
The ordered set A of nonzero real numbers

A = (−∞, 0) ∪ (0, +∞)

is not a linear continuum. Property b) is trivially satisfied. However, if B is the set of negative real numbers:

B = (−∞, 0)

then B is a subset of A which is bounded above (by any element of A greater than 0; for instance 1), but has no least upper bound in B. Notice that 0 is not a bound for B since 0 is not an element of A.

Let Z₋ denote the set of negative integers and let A = (0, 5) ∪ (5, +∞). Let

S = Z₋ ∪ A.

Then S satisfies neither property a) nor property b). The proof is similar to the previous examples.

Topological properties

Even though linear continua are important in the study of ordered sets, they do have applications in the mathematical field of topology. In fact, we will prove that an ordered set in the order topology is connected if and only if it is a linear continuum. We will prove one implication, and leave the other one as an exercise. (Munkres explains the second part of the proof in ^[3])

Theorem

Let X be an ordered set in the order topology. If X is connected, then X is a linear continuum.

Proof:

Suppose that x and y are elements of X with x < y. If there exists no z in X such that x < z < y, consider the sets:

A = (−∞, y)

B = (x, +∞)

These sets are disjoint (If a is in A, a < y so that if a is in B, a > x and a < y which is impossible by hypothesis), nonempty (x is in A and y is in B) and open (in the order topology), and their union is X. This contradicts the connectedness of X.

Now we prove the least upper bound property. If C is a subset of X that is bounded above and has no least upper bound, let D be the union of all open rays of the form (b, +∞) where b is an upper bound for C. Then D is open (since it is the union of open sets), and closed (if a is not in D, then a<b for all upper bounds b of C so that we may choose q>a such that q is in C (if no such q exists, a is the least upper bound of C), then an open interval containing a may be chosen that doesn't intersect D). Since D is nonempty (there is more than one upper bound of D for if there was exactly one upper bound s, s would be the least upper bound. Then if b₁ and b₂ are two upper bounds of D with b₁ < b₂, b₂ will belong to D), D and its complement together form a separation on X. This contradicts the connectedness of X.

Applications of the theorem

Since the ordered set A = (−∞, 0) U (0,+∞) is not a linear continuum, it is disconnected.
By applying the theorem just proved, the fact that R is connected follows. In fact any interval (or ray) in R is also connected.
The set of integers is not a linear continuum and therefore cannot be connected.
In fact, if an ordered set in the order topology is a linear continuum, it must be connected. Since any interval in this set is also a linear continuum, it follows that this space is locally connected since it has a basis consisting entirely of connected sets.
For an example of a topological space that is a linear continuum, see long line.

Related Research Articles

<span class="mw-page-title-main">Compact space</span> Type of mathematical space

In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers $is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers is not compact either, because it excludes the two limiting values and . However, the extended real number line would be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces.$

In mathematics, a set $B$ of vectors in a vector space $V$ is called a basis if every element of $V$ may be written in a unique way as a finite linear combination of elements of $B$ . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to $B$ . The elements of a basis are called basis vectors.

In mathematics, a total or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation $on some set, which satisfies the following for all and in :$

$(reflexive).$
If $and then (transitive).$
If $and then (antisymmetric).$
$or .$

This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In mathematics, a well-order on a set S is a total order on S with the property that every non-empty subset of S has a least element in this ordering. The set S together with the well-order relation is then called a well-ordered set. In some academic articles and textbooks these terms are instead written as wellorder, wellordered, and wellordering or well order, well ordered, and well ordering.

In mathematics, the infimum of a subset $of a partially ordered set is a greatest element in that is less than or equal to each element of if such an element exists. Consequently, the term greatest lower bound is also commonly used. The supremum of a subset of a partially ordered set is the least element in that is greater than or equal to each element of if such an element exists. Consequently, the supremum is also referred to as the least upper bound .$

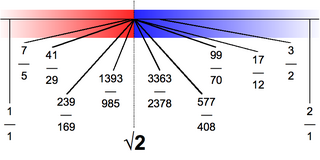
In mathematics, Dedekind cuts, named after German mathematician Richard Dedekind but previously considered by Joseph Bertrand, are а method of construction of the real numbers from the rational numbers. A Dedekind cut is a partition of the rational numbers into two sets A and B, such that all elements of A are less than all elements of B, and A contains no greatest element. The set B may or may not have a smallest element among the rationals. If B has a smallest element among the rationals, the cut corresponds to that rational. Otherwise, that cut defines a unique irrational number which, loosely speaking, fills the "gap" between A and B. In other words, A contains every rational number less than the cut, and B contains every rational number greater than or equal to the cut. An irrational cut is equated to an irrational number which is in neither set. Every real number, rational or not, is equated to one and only one cut of rationals.

In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers $x$ satisfying $0 \leq x \leq 1$ is an interval which contains $0$ , $1$ , and all numbers in between. Other examples of intervals are the set of numbers such that $0 < x < 1$ , the set of all real numbers $, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton.$

In mathematics, the well-ordering principle states that every non-empty set of positive integers contains a least element. In other words, the set of positive integers is well-ordered by its "natural" or "magnitude" order in which $precedes if and only if is either or the sum of and some positive integer.$

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.

In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets.

<span class="mw-page-title-main">Archimedean property</span> Mathematical property of algebraic structures

In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some algebraic structures, such as ordered or normed groups, and fields. The property, typically construed, states that given two positive numbers $and, there is an integer such that . It also means that the set of natural numbers is not bounded above. Roughly speaking, it is the property of having no infinitely large or infinitely small elements. It was Otto Stolz who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes’ On the Sphere and Cylinder .$

In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a point.

In mathematics, there are several equivalent ways of defining the real numbers. One of them is that they form a complete ordered field that does not contain any smaller complete ordered field. Such a definition does not prove that such a complete ordered field exists, and the existence proof consists of constructing a mathematical structure that satisfies the definition.

Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.

In general topology, a branch of mathematics, a non-empty family A of subsets of a set $is said to have the finite intersection property (FIP) if the intersection over any finite subcollection of is non-empty. It has the strong finite intersection property (SFIP) if the intersection over any finite subcollection of is infinite. Sets with the finite intersection property are also called centered systems and filter subbases .$

In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a distance, duration or temperature. Here, continuous means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion.

In mathematics, the least-upper-bound property is a fundamental property of the real numbers. More generally, a partially ordered set $X$ has the least-upper-bound property if every non-empty subset of $X$ with an upper bound has a least upper bound (supremum) in $X$ . Not every (partially) ordered set has the least upper bound property. For example, the set $of all rational numbers with its natural order does not have the least upper bound property.$

In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it. Formally, $is dense in if the smallest closed subset of containing is itself.$

Completeness is a property of the real numbers that, intuitively, implies that there are no "gaps" or "missing points" in the real number line. This contrasts with the rational numbers, whose corresponding number line has a "gap" at each irrational value. In the decimal number system, completeness is equivalent to the statement that any infinite string of decimal digits is actually a decimal representation for some real number.

References

↑ Munkres, James (2000). Topology, 2nd ed. Pearson Education. pp. 31, 153. ISBN 0-13-181629-2.
↑ Hardy, G.H. (1952). A Course of Pure Mathematics, 10th ed. Cambridge University Press. pp. 11–15, 24–31. ISBN 0-521-09227-2.
↑ Munkres, James (2000). Topology, 2nd ed. Pearson Education. pp. 153–154. ISBN 0-13-181629-2.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Munkres, James (2000). Topology, 2nd ed. Pearson Education. pp. 31, 153. ISBN 0-13-181629-2.

[2] Hardy, G.H. (1952). A Course of Pure Mathematics, 10th ed. Cambridge University Press. pp. 11–15, 24–31. ISBN 0-521-09227-2.

[3] Munkres, James (2000). Topology, 2nd ed. Pearson Education. pp. 153–154. ISBN 0-13-181629-2.

[1]

[2]

[3]