This article needs additional citations for verification .(April 2010) |

This is a list of complexity classes in computational complexity theory. For other computational and complexity subjects, see list of computability and complexity topics.
Many of these classes have a 'co' partner which consists of the complements of all languages in the original class. For example, if a language L is in NP then the complement of L is in co-NP. (This does not mean that the complement of NP is co-NP—there are languages which are known to be in both, and other languages which are known to be in neither.)
"The hardest problems" of a class refer to problems which belong to the class such that every other problem of that class can be reduced to it. Furthermore, the reduction is also a problem of the given class, or its subset.
| #P | Count solutions to an NP problem |
| #P-complete | The hardest problems in #P |
| 2-EXPTIME | Solvable in doubly exponential time |
| AC0 | A circuit complexity class of bounded depth |
| ACC0 | A circuit complexity class of bounded depth and counting gates |
| AC | A circuit complexity class |
| AH | The arithmetic hierarchy |
| AP | The class of problems alternating Turing machines can solve in polynomial time. [1] |
| APX | Optimization problems that have approximation algorithms with constant approximation ratio [1] |
| AM | Solvable in polynomial time by an Arthur–Merlin protocol [1] |
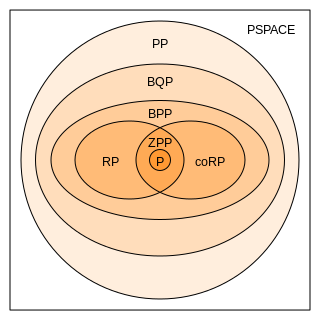
| BPP | Solvable in polynomial time by randomized algorithms (answer is probably right) |
| BQP | Solvable in polynomial time on a quantum computer (answer is probably right) |
| co-NP | "NO" answers checkable in polynomial time by a non-deterministic machine |
| co-NP-complete | The hardest problems in co-NP |
| DSPACE(f(n)) | Solvable by a deterministic machine with space O(f(n)). |
| DTIME(f(n)) | Solvable by a deterministic machine in time O(f(n)). |
| E | Solvable in exponential time with linear exponent |
| ELEMENTARY | The union of the classes in the exponential hierarchy |
| ESPACE | Solvable with exponential space with linear exponent |
| EXP | Same as EXPTIME |
| EXPSPACE | Solvable with exponential space |
| EXPTIME | Solvable in exponential time |
| FNP | The analogue of NP for function problems |
| FP | The analogue of P for function problems |
| FPNP | The analogue of PNP for function problems; the home of the traveling salesman problem |
| FPT | Fixed-parameter tractable |
| GapL | Logspace-reducible to computing the integer determinant of a matrix |
| IP | Solvable in polynomial time by an interactive proof system |
| L | Solvable with logarithmic (small) space |
| LOGCFL | Logspace-reducible to a context-free language |
| MA | Solvable in polynomial time by a Merlin–Arthur protocol |
| NC | Solvable efficiently (in polylogarithmic time) on parallel computers |
| NE | Solvable by a non-deterministic machine in exponential time with linear exponent |
| NESPACE | Solvable by a non-deterministic machine with exponential space with linear exponent |
| NEXP | Same as NEXPTIME |
| NEXPSPACE | Solvable by a non-deterministic machine with exponential space |
| NEXPTIME | Solvable by a non-deterministic machine in exponential time |
| NL | "YES" answers checkable with logarithmic space |
| NONELEMENTARY | Complement of ELEMENTARY. |
| NP | "YES" answers checkable in polynomial time (see complexity classes P and NP) |
| NP-complete | The hardest or most expressive problems in NP |
| NP-easy | Analogue to PNP for function problems; another name for FPNP |
| NP-equivalent | The hardest problems in FPNP |
| NP-hard | At least as hard as every problem in NP but not known to be in the same complexity class |
| NSPACE(f(n)) | Solvable by a non-deterministic machine with space O(f(n)). |
| NTIME(f(n)) | Solvable by a non-deterministic machine in time O(f(n)). |
| P | Solvable in polynomial time |
| P-complete | The hardest problems in P to solve on parallel computers |
| P/poly | Solvable in polynomial time given an "advice string" depending only on the input size |
| PCP | Probabilistically Checkable Proof |
| PH | The union of the classes in the polynomial hierarchy |
| PNP | Solvable in polynomial time with an oracle for a problem in NP; also known as Δ2P |
| PP | Probabilistically Polynomial (answer is right with probability slightly more than ½) |
| PPAD | Polynomial Parity Arguments on Directed graphs |
| PR | Solvable by recursively building up arithmetic functions. |
| PSPACE | Solvable with polynomial space. |
| PSPACE-complete | The hardest problems in PSPACE. |
| PTAS | Polynomial-time approximation scheme (a subclass of APX). |
| QIP | Solvable in polynomial time by a quantum interactive proof system. |
| QMA | Quantum analog of NP. |
| R | Solvable in a finite amount of time. |
| RE | Problems to which we can answer "YES" in a finite amount of time, but a "NO" answer might never come. |
| RL | Solvable with logarithmic space by randomized algorithms (NO answer is probably right, YES is certainly right) |
| RP | Solvable in polynomial time by randomized algorithms (NO answer is probably right, YES is certainly right) |
| SL | Problems log-space reducible to determining if a path exist between given vertices in an undirected graph. In October 2004 it was discovered that this class is in fact equal to L. |
| S2P | one round games with simultaneous moves refereed deterministically in polynomial time [2] |
| TFNP | Total function problems solvable in non-deterministic polynomial time. A problem in this class has the property that every input has an output whose validity may be checked efficiently, and the computational challenge is to find a valid output. |
| UP | Unambiguous Non-Deterministic Polytime functions. |
| ZPL | Solvable by randomized algorithms (answer is always right, average space usage is logarithmic) |
| ZPP | Solvable by randomized algorithms (answer is always right, average running time is polynomial) |