In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term atomic orbital may also refer to the physical region or space where the electron can be calculated to be present, as predicted by the particular mathematical form of the orbital.

A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. The equation is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In quantum physics, a wave function is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters ψ and Ψ.

In quantum physics and chemistry, quantum numbers describe values of conserved quantities in the dynamics of a quantum system. Quantum numbers correspond to eigenvalues of operators that commute with the Hamiltonian—quantities that can be known with precision at the same time as the system's energy—and their corresponding eigenspaces. Together, a specification of all of the quantum numbers of a quantum system fully characterize a basis state of the system, and can in principle be measured together.
In quantum mechanics, the principal quantum number is one of four quantum numbers assigned to each electron in an atom to describe that electron's state. Its values are natural numbers making it a discrete variable.

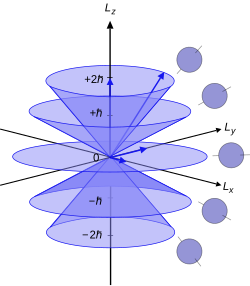
In quantum mechanics, the azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron. It is also known as the orbital angular momentum quantum number, orbital quantum number, subsidiary quantum number, or second quantum number, and is symbolized as ℓ.
In quantum mechanics, a rotational transition is an abrupt change in angular momentum. Like all other properties of a quantum particle, angular momentum is quantized, meaning it can only equal certain discrete values, which correspond to different rotational energy states. When a particle loses angular momentum, it is said to have transitioned to a lower rotational energy state. Likewise, when a particle gains angular momentum, a positive rotational transition is said to have occurred.
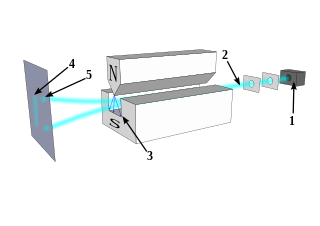
The Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment are deflected, due to the magnetic field gradient, from a straight path. The screen reveals discrete points of accumulation, rather than a continuous distribution, owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.
In physics, the spin quantum number is a quantum number that describes the intrinsic angular momentum of an electron or other particle. It has the same value for all particles of the same type, such as s = 1/2 for all electrons. It is an integer for all bosons, such as photons, and a half-odd-integer for all fermions, such as electrons and protons. The component of the spin along a specified axis is given by the spin magnetic quantum number, conventionally written ms. The value of ms is the component of spin angular momentum, in units of the reduced Planck constant ħ, parallel to a given direction. It can take values ranging from +s to −s in integer increments. For an electron, ms can be either ++1/2 or −+1/2.
The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was rather a set of heuristic corrections to classical mechanics. The theory is now understood as the semi-classical approximation to modern quantum mechanics. The main and final accomplishments of the old quantum theory were the determination of the modern form of the periodic table by Edmund Stoner and the Pauli Exclusion Principle which were both premised on the Arnold Sommerfeld enhancements to the Bohr model of the atom.
In atomic physics, a term symbol is an abbreviated description of the total spin and orbital angular momentum quantum numbers of the electrons in a multi-electron atom. So while the word symbol suggests otherwise, it represents an actual value of a physical quantity.
In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin and electric charge. The value of the electron magnetic moment is −9.2847647043(28)×10−24 J⋅T−1. In units of the Bohr magneton (μB), it is −1.00115965218059(13) μB, a value that was measured with a relative accuracy of 1.3×10−13.
In molecular physics, the molecular term symbol is a shorthand expression of the group representation and angular momenta that characterize the state of a molecule, i.e. its electronic quantum state which is an eigenstate of the electronic molecular Hamiltonian. It is the equivalent of the term symbol for the atomic case. However, the following presentation is restricted to the case of homonuclear diatomic molecules, or other symmetric molecules with an inversion centre. For heteronuclear diatomic molecules, the u/g symbol does not correspond to any exact symmetry of the electronic molecular Hamiltonian. In the case of less symmetric molecules the molecular term symbol contains the symbol of the group representation to which the molecular electronic state belongs.
In quantum physics, the spin–orbit interaction is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two relativistic effects: the apparent magnetic field seen from the electron perspective and the magnetic moment of the electron associated with its intrinsic spin. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin–orbit effects for electrons in semiconductors and other materials are explored for technological applications. The spin–orbit interaction is at the origin of magnetocrystalline anisotropy and the spin Hall effect.
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Such an operator is applied to a mathematical representation of the physical state of a system and yields an angular momentum value if the state has a definite value for it. In both classical and quantum mechanical systems, angular momentum is one of the three fundamental properties of motion.
The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photons, which are relativistic particles with dynamics described by Maxwell's equations, as an analogue for all types of particles.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.