
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

In physics, the Rabi cycle is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an optical driving field. The effect is important in quantum optics, magnetic resonance and quantum computing, and is named after Isidor Isaac Rabi.
In physics, a wave vector is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave, and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation.
In applied mathematics, the complex Mexican hat wavelet is a low-oscillation, complex-valued, wavelet for the continuous wavelet transform. This wavelet is formulated in terms of its Fourier transform as the Hilbert analytic signal of the conventional Mexican hat wavelet:

In probability theory, the Rice distribution or Rician distribution is the probability distribution of the magnitude of a circularly-symmetric bivariate normal random variable, possibly with non-zero mean (noncentral). It was named after Stephen O. Rice (1907–1986).
In functional analysis, the Shannon wavelet is a decomposition that is defined by signal analysis by ideal bandpass filters. Shannon wavelet may be either of real or complex type.
The Mathieu equation is a linear second-order differential equation with periodic coefficients. The French mathematician, E. Léonard Mathieu, first introduced this family of differential equations, nowadays termed Mathieu equations, in his “Memoir on vibrations of an elliptic membrane” in 1868. "Mathieu functions are applicable to a wide variety of physical phenomena, e.g., diffraction, amplitude distortion, inverted pendulum, stability of a floating body, radio frequency quadrupole, and vibration in a medium with modulated density"
In functional analysis, compactly supported wavelets derived from Legendre polynomials are termed Legendre wavelets or spherical harmonic wavelets. Legendre functions have widespread applications in which spherical coordinate system is appropriate. As with many wavelets there is no nice analytical formula for describing these harmonic spherical wavelets. The low-pass filter associated to Legendre multiresolution analysis is a finite impulse response (FIR) filter.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
Amplitude amplification is a technique in quantum computing which generalizes the idea behind Grover's search algorithm, and gives rise to a family of quantum algorithms. It was discovered by Gilles Brassard and Peter Høyer in 1997, and independently rediscovered by Lov Grover in 1998.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
The Bowring series of the transverse mercator published in 1989 by Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
In quantum field theory, and especially in quantum electrodynamics, the interacting theory leads to infinite quantities that have to be absorbed in a renormalization procedure, in order to be able to predict measurable quantities. The renormalization scheme can depend on the type of particles that are being considered. For particles that can travel asymptotically large distances, or for low energy processes, the on-shell scheme, also known as the physical scheme, is appropriate. If these conditions are not fulfilled, one can turn to other schemes, like the minimal subtraction scheme.
Fractional wavelet transform (FRWT) is a generalization of the classical wavelet transform (WT). This transform is proposed in order to rectify the limitations of the WT and the fractional Fourier transform (FRFT). The FRWT inherits the advantages of multiresolution analysis of the WT and has the capability of signal representations in the fractional domain which is similar to the FRFT.
In mathematics, in functional analysis, several different wavelets are known by the name Poisson wavelet. In one context, the term "Poisson wavelet" is used to denote a family of wavelets labeled by the set of positive integers, the members of which are associated with the Poisson probability distribution. These wavelets were first defined and studied by Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso in 1995–96. In another context, the term refers to a certain wavelet which involves a form of the Poisson integral kernel. In still another context, the terminology is used to describe a family of complex wavelets indexed by positive integers which are connected with the derivatives of the Poisson integral kernel.
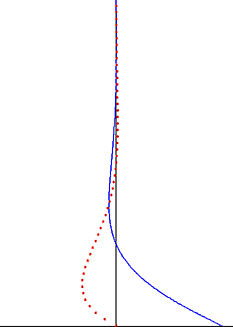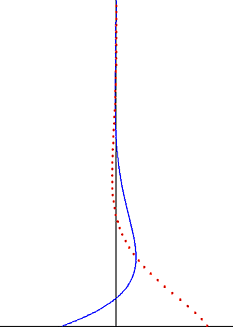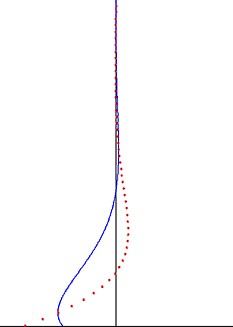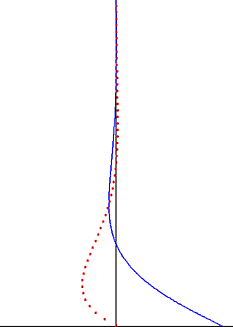
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered one of the simplest unsteady problems that has an exact solution for the Navier-Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.
In fluid dynamics, Beltrami flows are flows in which the vorticity vector and the velocity vector are parallel to each other. In other words, Beltrami flow is a flow where Lamb vector is zero. It is named after the Italian mathematician Eugenio Beltrami due to his derivation of the Beltrami vector field, while initial developments in fluid dynamics were done by the Russian scientist Ippolit S. Gromeka in 1881.
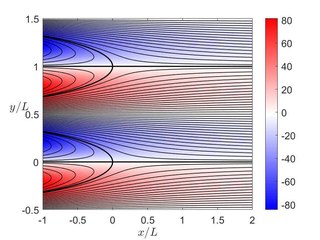
Kovasznay flow corresponds to an exact solution of the Navier–Stokes equations and are interpreted to describe the flow behind a two-dimensional grid. The flow is named after Leslie Stephen George Kovasznay, who discovered this solution in 1948. The solution is often used to validate numerical codes solving two-dimensional Navier-Stokes equations.


















