
A black hole is a region of spacetime where gravity is so strong that nothing, not even light and other electromagnetic waves, is capable of possessing enough energy to escape it. Einstein's theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole. The boundary of no escape is called the event horizon. A black hole has a great effect on the fate and circumstances of an object crossing it, but it has no locally detectable features according to general relativity. In many ways, a black hole acts like an ideal black body, as it reflects no light. Quantum field theory in curved spacetime predicts that event horizons emit Hawking radiation, with the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is of the order of billionths of a kelvin for stellar black holes, making it essentially impossible to observe directly.

General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations.
A wormhole is a hypothetical structure connecting disparate points in spacetime, and is based on a special solution of the Einstein field equations.

A gravitational singularity, spacetime singularity or simply singularity is a condition in which gravity is predicted to be so intense that spacetime itself would break down catastrophically. As such, a singularity is by definition no longer part of the regular spacetime and cannot be determined by "where" or "when". Gravitational singularities exist at a junction between general relativity and quantum mechanics; therefore, the properties of the singularity cannot be described without an established theory of quantum gravity. Trying to find a complete and precise definition of singularities in the theory of general relativity, the current best theory of gravity, remains a difficult problem. A singularity in general relativity can be defined by the scalar invariant curvature becoming infinite or, better, by a geodesic being incomplete.

Loop quantum gravity (LQG) is a theory of quantum gravity that incorporates matter of the Standard Model into the framework established for the intrinsic quantum gravity case. It is an attempt to develop a quantum theory of gravity based directly on Albert Einstein's geometric formulation rather than the treatment of gravity as a mysterious mechanism (force). As a theory, LQG postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. These networks of loops are called spin networks. The evolution of a spin network, or spin foam, has a scale on the order of a Planck length, approximately 10−35 meters, and smaller scales are meaningless. Consequently, not just matter, but space itself, prefers an atomic structure.
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory, is a classical theory of gravitation, one of several alternatives to general relativity. The theory was first proposed by Élie Cartan in 1922.
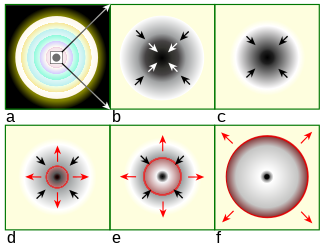
Gravitational collapse is the contraction of an astronomical object due to the influence of its own gravity, which tends to draw matter inward toward the center of gravity. Gravitational collapse is a fundamental mechanism for structure formation in the universe. Over time an initial, relatively smooth distribution of matter, after sufficient accretion, may collapse to form pockets of higher density, such as stars or black holes.
The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity (LQG), a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units. As a result, its value is currently fixed by matching the semiclassical black hole entropy, as calculated by Stephen Hawking, and the counting of microstates in loop quantum gravity.

In theoretical physics, quantum field theory in curved spacetime (QFTCS) is an extension of quantum field theory from Minkowski spacetime to a general curved spacetime. This theory uses a semi-classical approach; it treats spacetime as a fixed, classical background, while giving a quantum-mechanical description of the matter and energy propagating through that spacetime. A general prediction of this theory is that particles can be created by time-dependent gravitational fields (multigraviton pair production), or by time-independent gravitational fields that contain horizons. The most famous example of the latter is the phenomenon of Hawking radiation emitted by black holes.
Numerical relativity is one of the branches of general relativity that uses numerical methods and algorithms to solve and analyze problems. To this end, supercomputers are often employed to study black holes, gravitational waves, neutron stars and many other phenomena described by Einstein's theory of general relativity. A currently active field of research in numerical relativity is the simulation of relativistic binaries and their associated gravitational waves.
In acoustics and fluid dynamics, an acoustic metric is a metric that describes the signal-carrying properties of a given particulate medium.
A ring singularity or ringularity is the gravitational singularity of a rotating black hole, or a Kerr black hole, that is shaped like a ring.
In physics the Einstein-aether theory, also called aetheory, is the name coined in 2004 for a modification of general relativity that has a preferred reference frame and hence violates Lorentz invariance. These generally covariant theories describes a spacetime endowed with both a metric and a unit timelike vector field named the aether. The aether in this theory is "a Lorentz-violating vector field" unrelated to older luminiferous aether theories; the "Einstein" in the theory's name comes from its use of Einstein's general relativity equation.
In general relativity, an apparent horizon is a surface that is the boundary between light rays that are directed outwards and moving outwards and those directed outward but moving inward.
A nonsingular black hole model is a mathematical theory of black holes that avoids certain theoretical problems with the standard black hole model, including information loss and the unobservable nature of the black hole event horizon.

Relativistic images are images of gravitational lensing which result due to light deflections by angles .
In theoretical physics, a dynamical horizon (DH) is a local description of evolving black-hole horizons. In the literature there exist two different mathematical formulations of DHs—the 2+2 formulation developed first by Sean Hayward and the 3+1 formulation developed by Abhay Ashtekar and others. It provides a description of a black hole that is evolving. A related formalism, for black holes with zero influx, is an isolated horizon.
It was customary to represent black hole horizons via stationary solutions of field equations, i.e., solutions which admit a time-translational Killing vector field everywhere, not just in a small neighborhood of the black hole. While this simple idealization was natural as a starting point, it is overly restrictive. Physically, it should be sufficient to impose boundary conditions at the horizon which ensure only that the black hole itself is isolated. That is, it should suffice to demand only that the intrinsic geometry of the horizon be time independent, whereas the geometry outside may be dynamical and admit gravitational and other radiation.

In astrophysics, an extreme mass ratio inspiral (EMRI) is the orbit of a relatively light object around a much heavier object, that gradually spirals in due to the emission of gravitational waves. Such systems are likely to be found in the centers of galaxies, where stellar mass compact objects, such as stellar black holes and neutron stars, may be found orbiting a supermassive black hole. In the case of a black hole in orbit around another black hole this is an extreme mass ratio binary black hole. The term EMRI is sometimes used as a shorthand to denote the emitted gravitational waveform as well as the orbit itself.



























