The nine dots puzzle is a mathematical puzzle whose task is to connect nine squarely arranged points with a pen by four (or fewer) straight lines without lifting the pen.
The puzzle has appeared under various other names over the years.
In 1867, in the French chess journal Le Sphinx, an intellectual precursor to the nine dots puzzle appeared credited to Sam Loyd. [1] [2] Said chess puzzle corresponds to a "64 dots puzzle", i.e., marking all dots of an 8-by-8 square lattice, with an added constraint. [lower-alpha 1]
In 1907, the nine dots puzzle appears in an interview with Sam Loyd in The Strand Magazine: [4] [2]
In the same year, the puzzle also appeared in A. Cyril Pearson's puzzle book. It was there named a charming puzzle and involved nine dots. [5] [2]
Both versions of the puzzle thereafter appeared in newspapers. From at least 1908, Loyd's egg-version ran as advertising for Elgin Creamery Co in Washington, DC., renamed to The Elgin Creamery Egg Puzzle. [6] From at least 1910, Pearson's "nine dots"-version appeared in puzzle sections. [7] [8] [9]
In 1914, Sam Loyd's Cyclopedia of Puzzles is published posthumously by his son (also named Sam Loyd). [10] The puzzle is therein explained as follows: [11] [2]
Sam Loyd's naming of the puzzle is an allusion to the story of Egg of Columbus. [12]
In the 1941 compilation The Puzzle-Mine: Puzzles Collected from the Works of the Late Henry Ernest Dudeney , the puzzle is attributed to Dudeney himself and not Loyd. [13] [ page needed ]
It is possible to mark off the nine dots in four lines. [14] To do so, one goes outside the confines of the square area defined by the nine dots themselves. The phrase thinking outside the box, used by management consultants in the 1970s and 1980s, is a restatement of the solution strategy. According to Daniel Kies, the puzzle seems hard because we commonly imagine a boundary around the edge of the dot array. [15]
The inherent difficulty of the puzzle has been studied in experimental psychology. [16] [17]
Various published solutions break the implicit rules of the puzzle in order to achieve a solution with even fewer than four lines. For instance, if the dots are assumed to have some finite size, rather than to be infinitesimally-small mathematical grid points, then it is possible to connect them with only three slightly-slanted lines. Or, if the line is allowed to be arbitrarily thick, then one line can cover all of the points. [18]
Another way to use only a single line involves rolling the paper into a three-dimensional cylinder, so that the dots align along a single helix (which, as a geodesic of the cylinder, could be considered to be in some sense a straight line). Thus a single line can be drawn connecting all nine dots—which would appear as three lines in parallel on the paper, when flattened out. [19] It is also possible to fold the paper flat, or to cut the paper into pieces and rearrange it, in such a way that the nine dots lie on a single line in the plane. [18]
Instead of the 3-by-3 square lattice, generalizations have been proposed in the form of the least amount of lines needed on an n-by-n square lattice. Or, in mathematical terminology, the minimum-segment unicursal polygonal path covering an n × n array of dots.
Various such extensions were stated as puzzles by Dudeney and Loyd with different added constraints. [21]
In 1955, Murray S. Klamkin showed that if n > 2, then 2n − 2 line segments are sufficient and conjectured that it is necessary too. [22] [21] In 1956, the conjecture was proven by John Selfridge. [23] [21] [2]
In 1970, Solomon W. Golomb and John Selfridge showed that the unicursal polygonal path of 2n − 2 segments exists on the n × n array for all n > 3 with the further constraint that the path be closed, i.e., it starts and ends at the same point. [21] Moreover, the further constraint that the closed path remain within the convex hull of the array of dots can be satisfied for all n > 5. Finally, various results for the a × b array of dots are proven. [3]
The nine dots puzzle can be generalized to higher dimensions, by simply defining the grid and asking to find (one of) the shortest polygonal chain(s) (i.e., the polygonal chain with the fewest edges) that visits all those points.
In 2020, it has been proven [24] that the optimal solution for the above-mentioned problem has exactly links, for every positive integer . The given constructive solution is a straight generalization of the well-known covering trail that solves the case.
Moreover, it is even possible to further extend the given optimization problem to any arbitrary grid , but only the easiest cases have been solved at present (e.g., in 2022 Rinaldi and Ripà showed that the solution for the case is a trail/cycle of length for every , while it is known that the optimal solution for the case has , or , or links).
The Nine Dots Prize, named after the puzzle, [25] is a competition-based prize for "creative thinking that tackles contemporary societal issues." [26] It is sponsored by the Kadas Prize Foundation and supported by the Cambridge University Press and the Centre for Research in the Arts, Social Sciences and Humanities at the University of Cambridge. [27]
Recreational mathematics is mathematics carried out for recreation (entertainment) rather than as a strictly research- and application-based professional activity or as a part of a student's formal education. Although it is not necessarily limited to being an endeavor for amateurs, many topics in this field require no knowledge of advanced mathematics. Recreational mathematics involves mathematical puzzles and games, often appealing to children and untrained adults and inspiring their further study of the subject.
Samuel Loyd was an American chess player, chess composer, puzzle author, and recreational mathematician. Loyd was born in Philadelphia but raised in New York City.
The tangram is a dissection puzzle consisting of seven flat polygons, called tans, which are put together to form shapes. The objective is to replicate a pattern generally found in a puzzle book using all seven pieces without overlap. Alternatively the tans can be used to create original minimalist designs that are either appreciated for their inherent aesthetic merits or as the basis for challenging others to replicate its outline. It is reputed to have been invented in China sometime around the late 18th century and then carried over to America and Europe by trading ships shortly after. It became very popular in Europe for a time, and then again during World War I. It is one of the most widely recognized dissection puzzles in the world and has been used for various purposes including amusement, art, and education.
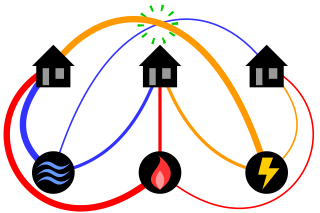
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.
Dynamic programming is both a mathematical optimization method and an algorithmic paradigm. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.
Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots are thought of as alphas (units). These are one type of 2-dimensional figurate numbers.
The 15 Puzzle is a sliding puzzle. It has 15 square tiles numbered 1 to 15 in a frame that is 4 tile positions high and 4 tile positions wide, with one unoccupied position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to place the tiles in numerical order.
Henry Ernest Dudeney was an English author and mathematician who specialised in logic puzzles and mathematical games. He is known as one of the country's foremost creators of mathematical puzzles.
Verbal arithmetic, also known as alphametics, cryptarithmetic, cryptarithm or word addition, is a type of mathematical game consisting of a mathematical equation among unknown numbers, whose digits are represented by letters of the alphabet. The goal is to identify the value of each letter. The name can be extended to puzzles that use non-alphabetic symbols instead of letters.
In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the number of stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as a three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorov, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope.
The no-three-in-line problem in discrete geometry asks how many points can be placed in the grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".
A dissection puzzle, also called a transformation puzzle or Richter puzzle, is a tiling puzzle where a set of pieces can be assembled in different ways to produce two or more distinct geometric shapes. The creation of new dissection puzzles is also considered to be a type of dissection puzzle. Puzzles may include various restraints, such as hinged pieces, pieces that can fold, or pieces that can twist. Creators of new dissection puzzles emphasize using a minimum number of pieces, or creating novel situations, such as ensuring that every piece connects to another with a hinge.
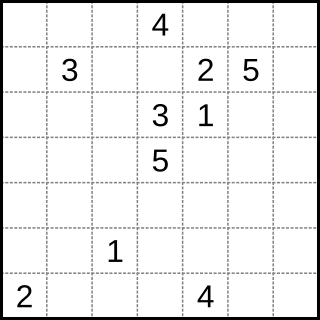
Numberlink is a type of logic puzzle involving finding paths to connect numbers in a grid.
In combinatorial mathematics, block walking is a method useful in thinking about sums of combinations graphically as "walks" on Pascal's triangle. As the name suggests, block walking problems involve counting the number of ways an individual can walk from one corner A of a city block to another corner B of another city block given restrictions on the number of blocks the person may walk, the directions the person may travel, the distance from A to B, et cetera.
Thinking outside the box is a metaphor that means to think differently, unconventionally, or from a new perspective. The phrase also often refers to novel or creative thinking.
In statistical mechanics, the two-dimensional square lattice Ising model is a simple lattice model of interacting magnetic spins. The model is notable for having nontrivial interactions, yet having an analytical solution. The model was solved by Lars Onsager for the special case that the external magnetic field H = 0. An analytical solution for the general case for has yet to be found.
In combinatorics, a lattice pathL in the d-dimensional integer lattice of length k with steps in the set S, is a sequence of vectors such that each consecutive difference lies in S. A lattice path may lie in any lattice in , but the integer lattice is most commonly used.
Placer la Dame ot l'on voudra, lui faire parcourir par des marches suivies et régulières toutes les cases de I'échiquier, et la ramener au quatorzième coup à son point de départ. Place the queen wherever you want, make her go through all the squares of the chessboard by regular steps, and bring her back to her starting point at the fourteenth move.
