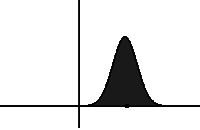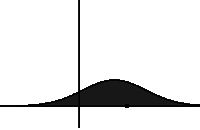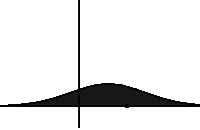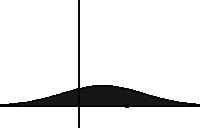
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker-Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc.

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter and a scale parameter .
- With a shape parameter and an inverse scale parameter , called a rate parameter.
The Green–Kubo relations give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions:
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
Differential entropy is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy, a measure of average (surprisal) of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula, and rather just assumed it was the correct continuous analogue of discrete entropy, but it is not. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy is commonly encountered in the literature, but it is a limiting case of the LDDP, and one that loses its fundamental association with discrete entropy.
In statistical mechanics, the Rushbrooke inequality relates the critical exponents of a magnetic system which exhibits a first-order phase transition in the thermodynamic limit for non-zero temperature T.
Continuous wavelets of compact support alpha can be built, which are related to the beta distribution. The process is derived from probability distributions using blur derivative. These new wavelets have just one cycle, so they are termed unicycle wavelets. They can be viewed as a soft variety of Haar wavelets whose shape is fine-tuned by two parameters and . Closed-form expressions for beta wavelets and scale functions as well as their spectra are derived. Their importance is due to the Central Limit Theorem by Gnedenko and Kolmogorov applied for compactly supported signals.
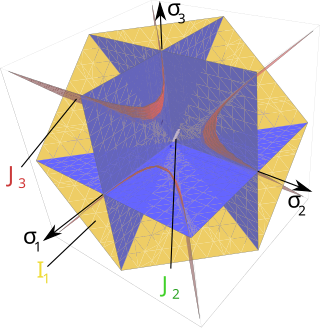
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
Superstatistics is a branch of statistical mechanics or statistical physics devoted to the study of non-linear and non-equilibrium systems. It is characterized by using the superposition of multiple differing statistical models to achieve the desired non-linearity. In terms of ordinary statistical ideas, this is equivalent to compounding the distributions of random variables and it may be considered a simple case of a doubly stochastic model.

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.
In computer networks, self-similarity is a feature of network data transfer dynamics. When modeling network data dynamics the traditional time series models, such as an autoregressive moving average model are not appropriate. This is because these models only provide a finite number of parameters in the model and thus interaction in a finite time window, but the network data usually have a long-range dependent temporal structure. A self-similar process is one way of modeling network data dynamics with such a long range correlation. This article defines and describes network data transfer dynamics in the context of a self-similar process. Properties of the process are shown and methods are given for graphing and estimating parameters modeling the self-similarity of network data.
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product is a product distribution.
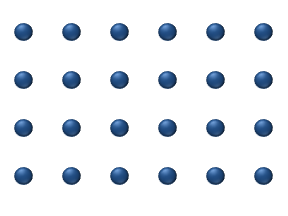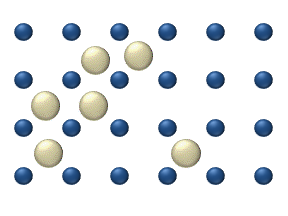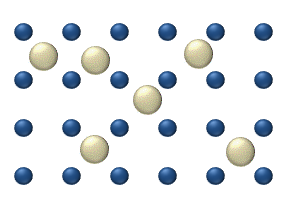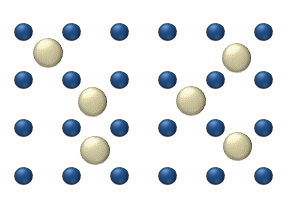
In statistical mechanics, thermal fluctuations are random deviations of an atomic system from its average state, that occur in a system at equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they decrease as temperature approaches absolute zero.
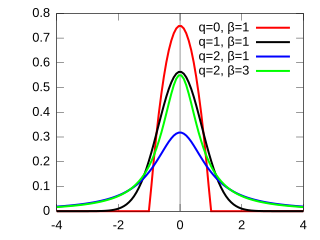
The q-Gaussian is a probability distribution arising from the maximization of the Tsallis entropy under appropriate constraints. It is one example of a Tsallis distribution. The q-Gaussian is a generalization of the Gaussian in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy. The normal distribution is recovered as q → 1.

The q-exponential distribution is a probability distribution arising from the maximization of the Tsallis entropy under appropriate constraints, including constraining the domain to be positive. It is one example of a Tsallis distribution. The q-exponential is a generalization of the exponential distribution in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy. The exponential distribution is recovered as
In probability and statistics, the generalized beta distribution is a continuous probability distribution with four shape parameters, including more than thirty named distributions as limiting or special cases. It has been used in the modeling of income distribution, stock returns, as well as in regression analysis. The exponential generalized beta (EGB) distribution follows directly from the GB and generalizes other common distributions.
The self-consistency principle was established by Rolf Hagedorn in 1965 to explain the thermodynamics of fireballs in high energy physics collisions. A thermodynamical approach to the high energy collisions first proposed by E. Fermi.

The Kaniadakis Gaussian distribution is a probability distribution which arises as a generalization of the Gaussian distribution from the maximization of the Kaniadakis entropy under appropriated constraints. It is one example of a Kaniadakis κ-distribution. The κ-Gaussian distribution has been applied successfully for describing several complex systems in economy, geophysics, astrophysics, among many others.