
The Chomsky hierarchy in the fields of formal language theory, computer science, and linguistics, is a containment hierarchy of classes of formal grammars. A formal grammar describes how to form strings from a language's vocabulary that are valid according to the language's syntax. The linguist Noam Chomsky theorized that four different classes of formal grammars existed that could generate increasingly complex languages. Each class can also completely generate the language of all inferior classes.
In formal language theory, a context-sensitive language is a language that can be defined by a context-sensitive grammar. Context-sensitive is known as type-1 in the Chomsky hierarchy of formal languages.
GNU Bison, commonly known as Bison, is a parser generator that is part of the GNU Project. Bison reads a specification in Bison syntax, warns about any parsing ambiguities, and generates a parser that reads sequences of tokens and decides whether the sequence conforms to the syntax specified by the grammar.
In computer science, an LL parser is a top-down parser for a restricted context-free language. It parses the input from Left to right, performing Leftmost derivation of the sentence.
In computer science, Backus–Naur form is a notation used to describe the syntax of programming languages or other formal languages. It was developed by John Backus and Peter Naur. BNF can be described as a metasyntax notation for context-free grammars. Backus–Naur form is applied wherever exact descriptions of languages are needed, such as in official language specifications, in manuals, and in textbooks on programming language theory. BNF can be used to describe document formats, instruction sets, and communication protocols.
In computer science, a recursive descent parser is a kind of top-down parser built from a set of mutually recursive procedures where each such procedure implements one of the nonterminals of the grammar. Thus the structure of the resulting program closely mirrors that of the grammar it recognizes.
Parsing, syntax analysis, or syntactic analysis is the process of analyzing a string of symbols, either in natural language, computer languages or data structures, conforming to the rules of a formal grammar. The term parsing comes from Latin pars (orationis), meaning part.
Top-down parsing in computer science is a parsing strategy where one first looks at the highest level of the parse tree and works down the parse tree by using the rewriting rules of a formal grammar. LL parsers are a type of parser that uses a top-down parsing strategy.
In computer science, a parsing expression grammar (PEG) is a type of analytic formal grammar, i.e. it describes a formal language in terms of a set of rules for recognizing strings in the language. The formalism was introduced by Bryan Ford in 2004 and is closely related to the family of top-down parsing languages introduced in the early 1970s. Syntactically, PEGs also look similar to context-free grammars (CFGs), but they have a different interpretation: the choice operator selects the first match in PEG, while it is ambiguous in CFG. This is closer to how string recognition tends to be done in practice, e.g. by a recursive descent parser.
The Packrat parser is a type of parser that shares similarities with the recursive descent parser in its construction. However, it differs because it takes parsing expression grammars (PEGs) as input rather than LL grammars.
In computer science, an operator precedence parser is a bottom-up parser that interprets an operator-precedence grammar. For example, most calculators use operator precedence parsers to convert from the human-readable infix notation relying on order of operations to a format that is optimized for evaluation such as Reverse Polish notation (RPN).
In the formal language theory of computer science, left recursion is a special case of recursion where a string is recognized as part of a language by the fact that it decomposes into a string from that same language and a suffix. For instance, can be recognized as a sum because it can be broken into , also a sum, and , a suitable suffix.
This is a list of notable lexer generators and parser generators for various language classes.

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.
META II is a domain-specific programming language for writing compilers. It was created in 1963–1964 by Dewey Val Schorre at UCLA. META II uses what Schorre called syntax equations. Its operation is simply explained as:
Each syntax equation is translated into a recursive subroutine which tests the input string for a particular phrase structure, and deletes it if found.
JetPAG is an open-source LL(k) parser and lexical analyzer generator, licensed under the GNU General Public License. It is a personal work of Tareq H. Sharafy, and is currently at final beta stages of development.
A syntactic predicate specifies the syntactic validity of applying a production in a formal grammar and is analogous to a semantic predicate that specifies the semantic validity of applying a production. It is a simple and effective means of dramatically improving the recognition strength of an LL parser by providing arbitrary lookahead. In their original implementation, syntactic predicates had the form “( α )?” and could only appear on the left edge of a production. The required syntactic condition α could be any valid context-free grammar fragment.
In computer programming, a parser combinator is a higher-order function that accepts several parsers as input and returns a new parser as its output. In this context, a parser is a function accepting strings as input and returning some structure as output, typically a parse tree or a set of indices representing locations in the string where parsing stopped successfully. Parser combinators enable a recursive descent parsing strategy that facilitates modular piecewise construction and testing. This parsing technique is called combinatory parsing.

A formal grammar describes which strings from an alphabet of a formal language are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form. A formal grammar is defined as a set of production rules for such strings in a formal language.
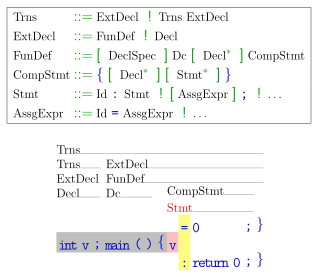
In formal language theory, an LL grammar is a context-free grammar that can be parsed by an LL parser, which parses the input from Left to right, and constructs a Leftmost derivation of the sentence. A language that has an LL grammar is known as an LL language. These form subsets of deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs), respectively. One says that a given grammar or language "is an LL grammar/language" or simply "is LL" to indicate that it is in this class.