 | This article may be too technical for most readers to understand.(April 2021) |
In materials science, a partial dislocation is a decomposed form of dislocation that occurs within a crystalline material. An extended dislocation is a dislocation that has dissociated into a pair of partial dislocations. The vector sum of the Burgers vectors of the partial dislocations is the Burgers vector of the extended dislocation.
A dislocation will decompose into partial dislocations if the energy state of the sum of the partials is less than the energy state of the original dislocation. This is summarized by Frank's Energy Criterion:
Shockley partial dislocations generally refer to a pair of dislocations which can lead to the presence of stacking faults. This pair of partial dislocations can enable dislocation motion by allowing an alternate path for atomic motion.
In FCC systems, an example of Shockley decomposition is:
Which is energetically favorable:
The components of the Shockley Partials must add up to the original vector that is being decomposed:
Frank partial dislocations are sessile (immobile), but can move by diffusion of atoms. [1] In FCC systems, Frank partials are given by:
For FCC crystals, Thompson tetrahedrons or Thompson notation are an invented notation for more easily describing partial dislocations. In a given unit cell, mark point A at the origin, point B at a/2 [110], point C at a/2[011], and point D at a/2[101]--these points form the vertices of a tetrahedron. Then, mark the center of the opposite faces for each point as α, β, γ, and δ, respectively. [2] With this, the geometric representation of a Thompson tetrahedron is complete.
Any combination of Roman letters describes a member of the {111} slip planes in an FCC crystal. A vector made from two Roman letters describes the Burgers vector of a perfect dislocation. If the vector is made from a Roman letter and a Greek letter, then it is a Frank partial if the letters are corresponding (Aα,Bβ,...) or a Shockley partial otherwise (Aβ, Aγ,...). Vectors made from two Greek letters describe stair-rod dislocations. Using Thompson notation, Burgers vectors can be added to describe other dislocations and mechanisms. For example, two Shockley partial dislocations can be added to form a perfect dislocation: Aβ + βC = AC. [2] It is necessary that the interior letters of a given operation match, but many can be added in sequence to describe more complex mechanisms.
It is useful to summarize this information using an unfolded Thompson tetrahedron.
The Lomer-Cottrell dislocation forms via a more complex dislocation reaction. For example, consider two extended dislocations: DB = Dγ + γB and BC = Bδ + δC. When they meet, it is more energetically favorable to form a single dislocation, DC = DB + BC = Dγ + γB + Bδ + δC = Dγ + γδ + δC. The trailing partials of each extended dislocation now form a stair-rod partial. This structure leads to reduced mobility of the dislocations as the core structure is non-planar (meaning it doesn’t cross along the face of the tetrahedron). [2] This reduction of mobility transforms the Lomer-Cottrell dislocation into an obstacle for other dislocations, thus strengthening the material.
When forming stacking faults, the partial dislocations reach an equilibrium when the repulsive energy between partial dislocations matches the attractive energy of the stacking fault. This means that higher stacking fault energy materials, i.e. those with high shear modulus and large Burgers vectors, will have smaller distance between partial dislocations. Conversely, low stacking fault energy materials will have large distances between partial dislocations. [3]
In order to cross slip, both partial dislocations need to change slip planes. The common Friedel-Escaig mechanism requires that the partial dislocations recombine at a point before cross slipping onto a different slip plane. [2] Bringing the partials together entails applying sufficient shear stress to reduce the distance between them, so partial dislocations with low stacking fault energies will inherently be more difficult to bring together and thus more difficult to cross slip. [3] [4] Conversely, high stacking fault energy materials will be easier to cross slip.
The more easily a dislocation can cross slip, the more freely the dislocation can move around obstacles–this makes work hardening more difficult. Thus, materials that allow easy cross slip (high stacking fault energy) will see less work hardening and strengthening from methods like solid-solution strengthening.
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
The stream function is defined for incompressible (divergence-free) flows in two dimensions – as well as in three dimensions with axisymmetry. The flow velocity components can be expressed as the derivatives of the scalar stream function. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. The two-dimensional Lagrange stream function was introduced by Joseph Louis Lagrange in 1781. The Stokes stream function is for axisymmetrical three-dimensional flow, and is named after George Gabriel Stokes.
In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.
A directional derivative is a concept in multivariable calculus that measures the rate at which a function changes in a particular direction at a given point.
The Reynolds-averaged Navier–Stokes equations are time-averaged equations of motion for fluid flow. The idea behind the equations is Reynolds decomposition, whereby an instantaneous quantity is decomposed into its time-averaged and fluctuating quantities, an idea first proposed by Osborne Reynolds. The RANS equations are primarily used to describe turbulent flows. These equations can be used with approximations based on knowledge of the properties of flow turbulence to give approximate time-averaged solutions to the Navier–Stokes equations. For a stationary flow of an incompressible Newtonian fluid, these equations can be written in Einstein notation in Cartesian coordinates as:
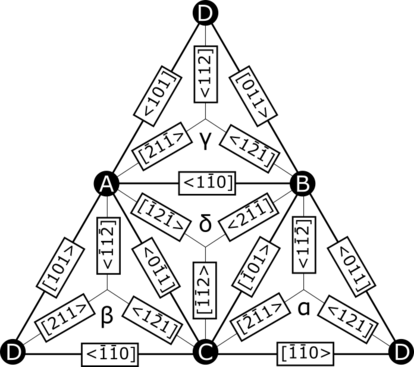
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as glide or slip. The crystalline order is restored on either side of a glide dislocation but the atoms on one side have moved by one position. The crystalline order is not fully restored with a partial dislocation. A dislocation defines the boundary between slipped and unslipped regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plastic deformation of a material occurs by the creation and movement of many dislocations. The number and arrangement of dislocations influences many of the properties of materials.
Large eddy simulation (LES) is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and first explored by Deardorff (1970). LES is currently applied in a wide variety of engineering applications, including combustion, acoustics, and simulations of the atmospheric boundary layer.
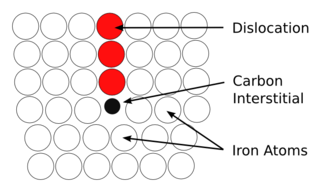
In materials science, the concept of the Cottrell atmosphere was introduced by A. H. Cottrell and B. A. Bilby in 1949 to explain how dislocations are pinned in some metals by boron, carbon, or nitrogen interstitials.
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.
In differential calculus, the Reynolds transport theorem, or simply the Reynolds theorem, named after Osborne Reynolds (1842–1912), is a three-dimensional generalization of the Leibniz integral rule. It is used to recast time derivatives of integrated quantities and is useful in formulating the basic equations of continuum mechanics.
In materials science, a Lomer–Cottrell junction is a particular configuration of dislocations.
In physics and continuum mechanics, deformation is the change in the shape or size of an object. It has dimension of length with SI unit of metre (m). It is quantified as the residual displacement of particles in a non-rigid body, from an initial configuration to a final configuration, excluding the body's average translation and rotation. A configuration is a set containing the positions of all particles of the body.
Dislocation creep is a deformation mechanism in crystalline materials. Dislocation creep involves the movement of dislocations through the crystal lattice of the material, in contrast to diffusion creep, in which diffusion is the dominant creep mechanism. It causes plastic deformation of the individual crystals, and thus the material itself.
An antiphase domain (APD) is a type of planar crystallographic defect in which the atoms within a region of a crystal are configured in the opposite order to those in the perfect lattice system. Throughout the entire APD, atoms sit on the sites typically occupied by atoms of a different species. For example, in an ordered AB alloy, if an A atom occupies the site usually occupied by a B atom, a type of crystallographic point defect called an antisite defect is formed. If an entire region of the crystal is translated such that every atom in a region of the plane of atoms sits on its antisite, an antiphase domain is formed. In other words, an APD is a region formed from antisite defects of a parent lattice. On either side of this domain, the lattice is still perfect, and the boundaries of the domain are referred to as antiphase boundaries. Crucially, crystals on either side of an antiphase boundary are related by a translation, rather than a reflection or an inversion.
Filtering in the context of large eddy simulation (LES) is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations. Because the principal difficulty in simulating turbulent flows comes from the wide range of length and time scales, this operation makes turbulent flow simulation cheaper by reducing the range of scales that must be resolved. The LES filter operation is low-pass, meaning it filters out the scales associated with high frequencies.
In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.
The acoustoelastic effect is how the sound velocities of an elastic material change if subjected to an initial static stress field. This is a non-linear effect of the constitutive relation between mechanical stress and finite strain in a material of continuous mass. In classical linear elasticity theory small deformations of most elastic materials can be described by a linear relation between the applied stress and the resulting strain. This relationship is commonly known as the generalised Hooke's law. The linear elastic theory involves second order elastic constants and yields constant longitudinal and shear sound velocities in an elastic material, not affected by an applied stress. The acoustoelastic effect on the other hand include higher order expansion of the constitutive relation between the applied stress and resulting strain, which yields longitudinal and shear sound velocities dependent of the stress state of the material. In the limit of an unstressed material the sound velocities of the linear elastic theory are reproduced.
In crystallography, a stacking fault is a planar defect that can occur in crystalline materials. Crystalline materials form repeating patterns of layers of atoms. Errors can occur in the sequence of these layers and are known as stacking faults. Stacking faults are in a higher energy state which is quantified by the formation enthalpy per unit area called the stacking-fault energy. Stacking faults can arise during crystal growth or from plastic deformation. In addition, dislocations in low stacking-fault energy materials typically dissociate into an extended dislocation, which is a stacking fault bounded by partial dislocations.
Geometrically necessary dislocations are like-signed dislocations needed to accommodate for plastic bending in a crystalline material. They are present when a material's plastic deformation is accompanied by internal plastic strain gradients. They are in contrast to statistically stored dislocations, with statistics of equal positive and negative signs, which arise during plastic flow from multiplication processes like the Frank-Read source.
