In mathematics, the geometric algebra (GA) of a vector space is an algebra over a field, noted for its multiplication operation called the geometric product on a space of elements called multivectors, which contains both the scalars and the vector space .
The Cauchy–Schwarz inequality is considered one of the most important and widely used inequalities in mathematics.

In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry, theoretical physics and digital image processing. They are named after the English mathematician William Kingdon Clifford.
In mathematics, a linear form is a linear map from a vector space to its field of scalars.
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F, or equivalently, a one-dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space V is a basis for V whose vectors are mutually orthogonal. If the vectors of an orthogonal basis are normalized, the resulting basis is an orthonormal basis.
In mathematics, the Lasker–Noether theorem states that every Noetherian ring is a Lasker ring, which means that every ideal can be decomposed as an intersection, called primary decomposition, of finitely many primary ideals. The theorem was first proven by Emanuel Lasker (1905) for the special case of polynomial rings and convergent power series rings, and was proven in its full generality by Emmy Noether (1921).
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes a matrix algebra by extending scalars, i.e. for a suitable field extension K of F, is isomorphic to the 2×2 matrix algebra over K.
In mathematics, Milnor K-theory is an algebraic invariant defined by John Milnor (1970) as an attempt to study higher algebraic K-theory in the special case of fields. It was hoped this would help illuminate the structure for algebraic K-theory and give some insight about its relationships with other parts of mathematics, such as Galois cohomology and the Grothendieck–Witt ring of quadratic forms. Before Milnor K-theory was defined, there existed ad-hoc definitions for and . Fortunately, it can be shown Milnor K-theory is a part of algebraic K-theory, which in general is the easiest part to compute.
In mathematics, a composition algebraA over a field K is a not necessarily associative algebra over K together with a nondegenerate quadratic form N that satisfies
In mathematics, a Witt group of a field, named after Ernst Witt, is an abelian group whose elements are represented by symmetric bilinear forms over the field.
In mathematics, an octonion algebra or Cayley algebra over a field F is an algebraic structure which is an 8-dimensional composition algebra over F. In other words, it is a unital non-associative algebra A over F with a non-degenerate quadratic form N such that
In mathematics, a quadratic form over a field F is said to be isotropic if there is a non-zero vector on which the form evaluates to zero. Otherwise the quadratic form is anisotropic. More precisely, if q is a quadratic form on a vector space V over F, then a non-zero vector v in V is said to be isotropic if q(v) = 0. A quadratic form is isotropic if and only if there exists a non-zero isotropic vector for that quadratic form.

In mathematics, more specifically abstract algebra and ring theory, a noncommutative ring is a ring whose multiplication is not commutative; that is, there exists a and b in R with a·b ≠ b·a. Many authors use the term noncommutative rings to refer to rings which are not necessarily commutative, and hence include commutative rings in their definition. Noncommutative algebra is the study of results applying to rings that are not required to be commutative. Many important results in the field of noncommutative algebra apply to commutative rings as special cases.
In mathematics, the norm residue isomorphism theorem is a long-sought result relating Milnor K-theory and Galois cohomology. The result has a relatively elementary formulation and at the same time represents the key juncture in the proofs of many seemingly unrelated theorems from abstract algebra, theory of quadratic forms, algebraic K-theory and the theory of motives. The theorem asserts that a certain statement holds true for any prime and any natural number . John Milnor speculated that this theorem might be true for and all , and this question became known as Milnor's conjecture. The general case was conjectured by Spencer Bloch and Kazuya Kato and became known as the Bloch–Kato conjecture or the motivic Bloch–Kato conjecture to distinguish it from the Bloch–Kato conjecture on values of L-functions. The norm residue isomorphism theorem was proved by Vladimir Voevodsky using a number of highly innovative results of Markus Rost.

Aleksandr Sergeyevich Merkurjev is a Russian-American mathematician, who has made major contributions to the field of algebra. Currently Merkurjev is a professor at the University of California, Los Angeles.
In mathematics, the universal invariant or u-invariant of a field describes the structure of quadratic forms over the field.
In mathematics, a biquaternion algebra is a compound of quaternion algebras over a field.
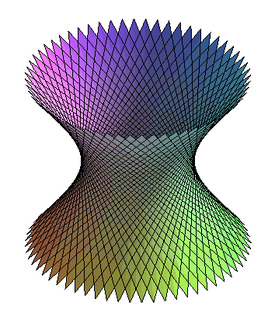
In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface










