A context-sensitive grammar (CSG) is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols. Context-sensitive grammars are more general than context-free grammars, in the sense that there are languages that can be described by a CSG but not by a context-free grammar. Context-sensitive grammars are less general than unrestricted grammars. Thus, CSGs are positioned between context-free and unrestricted grammars in the Chomsky hierarchy.

In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form
In formal language theory, a context-free language (CFL), also called a Chomsky type-2 language, is a language generated by a context-free grammar (CFG).
In formal language theory, a context-free grammar, G, is said to be in Chomsky normal form if all of its production rules are of the form:
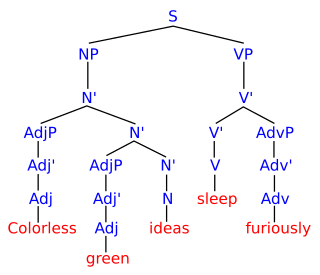
In logic, mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules called a formal grammar.

In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.
In computer science, an LL parser is a top-down parser for a restricted context-free language. It parses the input from Left to right, performing Leftmost derivation of the sentence.
In computer science, an ambiguous grammar is a context-free grammar for which there exists a string that can have more than one leftmost derivation or parse tree. Every non-empty context-free language admits an ambiguous grammar by introducing e.g. a duplicate rule. A language that only admits ambiguous grammars is called an inherently ambiguous language. Deterministic context-free grammars are always unambiguous, and are an important subclass of unambiguous grammars; there are non-deterministic unambiguous grammars, however.
Top-Down Parsing Language (TDPL) is a type of analytic formal grammar developed by Alexander Birman in the early 1970s in order to study formally the behavior of a common class of practical top-down parsers that support a limited form of backtracking. Birman originally named his formalism the TMG Schema (TS), after TMG, an early parser generator, but it was later given the name TDPL by Aho and Ullman in their classic anthology The Theory of Parsing, Translation and Compiling.
In computer science, a linear grammar is a context-free grammar that has at most one nonterminal in the right-hand side of each of its productions.
Conjunctive grammars are a class of formal grammars studied in formal language theory. They extend the basic type of grammars, the context-free grammars, with a conjunction operation. Besides explicit conjunction, conjunctive grammars allow implicit disjunction represented by multiple rules for a single nonterminal symbol, which is the only logical connective expressible in context-free grammars. Conjunction can be used, in particular, to specify intersection of languages. A further extension of conjunctive grammars known as Boolean grammars additionally allows explicit negation.
In formal language theory, an alphabet, sometimes called a vocabulary, is a non-empty set of indivisible symbols/glyphs, typically thought of as representing letters, characters, digits, phonemes, or even words. Alphabets in this technical sense of a set are used in a diverse range of fields including logic, mathematics, computer science, and linguistics. An alphabet may have any cardinality ("size") and, depending on its purpose, may be finite, countable, or even uncountable.
In computer science, in the area of formal language theory, frequent use is made of a variety of string functions; however, the notation used is different from that used for computer programming, and some commonly used functions in the theoretical realm are rarely used when programming. This article defines some of these basic terms.
In formal language theory, a grammar is noncontracting if for all of its production rules, α → β, it holds that |α| ≤ |β|, that is β has at least as many symbols as α. A grammar is essentially noncontracting if there may be one exception, namely, a rule S → ε where S is the start symbol and ε the empty string, and furthermore, S never occurs in the right-hand side of any rule.
Indexed grammars are a generalization of context-free grammars in that nonterminals are equipped with lists of flags, or index symbols. The language produced by an indexed grammar is called an indexed language.

A formal grammar describes which strings from an alphabet of a formal language are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form. A formal grammar is defined as a set of production rules for such strings in a formal language.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
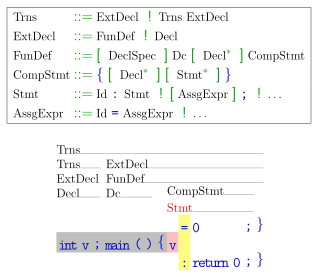
In formal language theory, an LL grammar is a context-free grammar that can be parsed by an LL parser, which parses the input from Left to right, and constructs a Leftmost derivation of the sentence. A language that has an LL grammar is known as an LL language. These form subsets of deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs), respectively. One says that a given grammar or language "is an LL grammar/language" or simply "is LL" to indicate that it is in this class.
In theoretical computer science, in particular in formal language theory, Greibach's theorem states that certain properties of formal language classes are undecidable. It is named after the computer scientist Sheila Greibach, who first proved it in 1963.






