Rijndael S-box

Last updated May 07, 2023

The Rijndael S-box is a substitution box (lookup table) used in the Rijndael cipher, on which the Advanced Encryption Standard (AES) cryptographic algorithm is based.^[1]

Forward S-box

AES S-box
	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
00	63	7c	77	7b	f2	6b	6f	c5	30	01	67	2b	fe	d7	ab	76
10	ca	82	c9	7d	fa	59	47	f0	ad	d4	a2	af	9c	a4	72	c0
20	b7	fd	93	26	36	3f	f7	cc	34	a5	e5	f1	71	d8	31	15
30	04	c7	23	c3	18	96	05	9a	07	12	80	e2	eb	27	b2	75
40	09	83	2c	1a	1b	6e	5a	a0	52	3b	d6	b3	29	e3	2f	84
50	53	d1	00	ed	20	fc	b1	5b	6a	cb	be	39	4a	4c	58	cf
60	d0	ef	aa	fb	43	4d	33	85	45	f9	02	7f	50	3c	9f	a8
70	51	a3	40	8f	92	9d	38	f5	bc	b6	da	21	10	ff	f3	d2
80	cd	0c	13	ec	5f	97	44	17	c4	a7	7e	3d	64	5d	19	73
90	60	81	4f	dc	22	2a	90	88	46	ee	b8	14	de	5e	0b	db
a0	e0	32	3a	0a	49	06	24	5c	c2	d3	ac	62	91	95	e4	79
b0	e7	c8	37	6d	8d	d5	4e	a9	6c	56	f4	ea	65	7a	ae	08
c0	ba	78	25	2e	1c	a6	b4	c6	e8	dd	74	1f	4b	bd	8b	8a
d0	70	3e	b5	66	48	03	f6	0e	61	35	57	b9	86	c1	1d	9e
e0	e1	f8	98	11	69	d9	8e	94	9b	1e	87	e9	ce	55	28	df
f0	8c	a1	89	0d	bf	e6	42	68	41	99	2d	0f	b0	54	bb	16
The column is determined by the least significant nibble, and the row by the most significant nibble. For example, the value 9a₁₆ is converted into b8₁₆.

The S-box maps an 8-bit input, $c$ , to an 8-bit output, $s = S (c)$ . Both the input and output are interpreted as polynomials over GF(2). First, the input is mapped to its multiplicative inverse in $GF(2 8) = GF(2) [x]/(x 8 + x 4 + x 3 + x + 1)$ , Rijndael's finite field. Zero, as the identity, is mapped to itself. This transformation is known as the Nyberg S-box after its inventor Kaisa Nyberg.^[2] The multiplicative inverse is then transformed using the following affine transformation:

{\begin{bmatrix}s_{0}\\s_{1}\\s_{2}\\s_{3}\\s_{4}\\s_{5}\\s_{6}\\s_{7}\end{bmatrix}}={\begin{bmatrix}1&0&0&0&1&1&1&1\\1&1&0&0&0&1&1&1\\1&1&1&0&0&0&1&1\\1&1&1&1&0&0&0&1\\1&1&1&1&1&0&0&0\\0&1&1&1&1&1&0&0\\0&0&1&1&1&1&1&0\\0&0&0&1&1&1&1&1\end{bmatrix}}{\begin{bmatrix}b_{0}\\b_{1}\\b_{2}\\b_{3}\\b_{4}\\b_{5}\\b_{6}\\b_{7}\end{bmatrix}}+{\begin{bmatrix}1\\1\\0\\0\\0\\1\\1\\0\end{bmatrix}}

where $[s 7, ..., s 0]$ is the S-box output and $[b 7, ..., b 0]$ is the multiplicative inverse as a vector.

This affine transformation is the sum of multiple rotations of the byte as a vector, where addition is the XOR operation:

s=b\oplus (b\lll 1)\oplus (b\lll 2)\oplus (b\lll 3)\oplus (b\lll 4)\oplus 63_{16}

where $b$ represents the multiplicative inverse, $\oplus$ is the bitwise XOR operator, $\lll$ is a left bitwise circular shift, and the constant $6316 = 01100011 2$ is given in hexadecimal.

An equivalent formulation of the affine transformation is

s_{i}=b_{i}\oplus b_{(i+4)\operatorname {mod} 8}\oplus b_{(i+5)\operatorname {mod} 8}\oplus b_{(i+6)\operatorname {mod} 8}\oplus b_{(i+7)\operatorname {mod} 8}\oplus c_{i}

where $s$ , $b$ , and $c$ are 8 bit arrays, $c$ is 01100011₂, and subscripts indicate a reference to the indexed bit.^[3]

Another equivalent is:

s=\left(b\times 31_{10}\mod {257_{10}}\right)\oplus 99_{10}

^[4]^[5]

where $\times$ is polynomial multiplication of $b$ and $31_{10}$ taken as bit arrays.

Inverse S-box

Inverse S-box
	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
00	52	09	6a	d5	30	36	a5	38	bf	40	a3	9e	81	f3	d7	fb
10	7c	e3	39	82	9b	2f	ff	87	34	8e	43	44	c4	de	e9	cb
20	54	7b	94	32	a6	c2	23	3d	ee	4c	95	0b	42	fa	c3	4e
30	08	2e	a1	66	28	d9	24	b2	76	5b	a2	49	6d	8b	d1	25
40	72	f8	f6	64	86	68	98	16	d4	a4	5c	cc	5d	65	b6	92
50	6c	70	48	50	fd	ed	b9	da	5e	15	46	57	a7	8d	9d	84
60	90	d8	ab	00	8c	bc	d3	0a	f7	e4	58	05	b8	b3	45	06
70	d0	2c	1e	8f	ca	3f	0f	02	c1	af	bd	03	01	13	8a	6b
80	3a	91	11	41	4f	67	dc	ea	97	f2	cf	ce	f0	b4	e6	73
90	96	ac	74	22	e7	ad	35	85	e2	f9	37	e8	1c	75	df	6e
a0	47	f1	1a	71	1d	29	c5	89	6f	b7	62	0e	aa	18	be	1b
b0	fc	56	3e	4b	c6	d2	79	20	9a	db	c0	fe	78	cd	5a	f4
c0	1f	dd	a8	33	88	07	c7	31	b1	12	10	59	27	80	ec	5f
d0	60	51	7f	a9	19	b5	4a	0d	2d	e5	7a	9f	93	c9	9c	ef
e0	a0	e0	3b	4d	ae	2a	f5	b0	c8	eb	bb	3c	83	53	99	61
f0	17	2b	04	7e	ba	77	d6	26	e1	69	14	63	55	21	0c	7d

The inverse S-box is simply the S-box run in reverse. For example, the inverse S-box of b8₁₆ is 9a₁₆. It is calculated by first calculating the inverse affine transformation of the input value, followed by the multiplicative inverse. The inverse affine transformation is as follows:

{\begin{bmatrix}b_{0}\\b_{1}\\b_{2}\\b_{3}\\b_{4}\\b_{5}\\b_{6}\\b_{7}\end{bmatrix}}={\begin{bmatrix}0&0&1&0&0&1&0&1\\1&0&0&1&0&0&1&0\\0&1&0&0&1&0&0&1\\1&0&1&0&0&1&0&0\\0&1&0&1&0&0&1&0\\0&0&1&0&1&0&0&1\\1&0&0&1&0&1&0&0\\0&1&0&0&1&0&1&0\end{bmatrix}}{\begin{bmatrix}s_{0}\\s_{1}\\s_{2}\\s_{3}\\s_{4}\\s_{5}\\s_{6}\\s_{7}\end{bmatrix}}+{\begin{bmatrix}1\\0\\1\\0\\0\\0\\0\\0\end{bmatrix}}

The inverse affine transformation also represents the sum of multiple rotations of the byte as a vector, where addition is the XOR operation:

b=(s\lll 1)\oplus (s\lll 3)\oplus (s\lll 6)\oplus 5_{16}

where $\oplus$ is the bitwise XOR operator, $\lll$ is a left bitwise circular shift, and the constant $516 = 00000101 2$ is given in hexadecimal.

Design criteria

The Rijndael S-box was specifically designed to be resistant to linear and differential cryptanalysis. This was done by minimizing the correlation between linear transformations of input/output bits, and at the same time minimizing the difference propagation probability.

The Rijndael S-box can be replaced in the Rijndael cipher,^[1] which defeats the suspicion of a backdoor built into the cipher that exploits a static S-box. The authors claim that the Rijndael cipher structure is likely to provide enough resistance against differential and linear cryptanalysis even if an S-box with "average" correlation / difference propagation properties is used (cf. the "optimal" properties of the Rijndael S-box).

Example implementation in C language

The following C code calculates the S-box:

#include<stdint.h>#define ROTL8(x,shift) ((uint8_t) ((x) << (shift)) | ((x) >> (8 - (shift))))voidinitialize_aes_sbox(uint8_tsbox[256]){uint8_tp=1,q=1;/* loop invariant: p * q == 1 in the Galois field */do{/* multiply p by 3 */p=p^(p<<1)^(p&0x80?0x1B:0);/* divide q by 3 (equals multiplication by 0xf6) */q^=q<<1;q^=q<<2;q^=q<<4;q^=q&0x80?0x09:0;/* compute the affine transformation */uint8_txformed=q^ROTL8(q,1)^ROTL8(q,2)^ROTL8(q,3)^ROTL8(q,4);sbox[p]=xformed^0x63;}while(p!=1);/* 0 is a special case since it has no inverse */sbox[0]=0x63;}

Related Research Articles

The Advanced Encryption Standard (AES), also known by its original name Rijndael, is a specification for the encryption of electronic data established by the U.S. National Institute of Standards and Technology (NIST) in 2001.

In cryptography, a block cipher is a deterministic algorithm operating on fixed-length groups of bits, called blocks. Block ciphers are specified elementary components in the design of many cryptographic protocols and are widely used to encrypt large amounts of data, including in data exchange protocols. A block cipher uses blocks as an unvarying transformation.

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.

In Euclidean geometry, an affine transformation or affinity is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.

<span class="mw-page-title-main">Exclusive or</span> True when either but not both inputs are true

Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ.

In computer programming, the exclusive or swap is an algorithm that uses the exclusive or bitwise operation to swap the values of two variables without using the temporary variable which is normally required.

In mathematics, the orthogonal group in dimension $, denoted, is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.$

In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operations and directly supported by the processor. Most bitwise operations are presented as two-operand instructions where the result replaces one of the input operands.

<span class="mw-page-title-main">Involution (mathematics)</span> Function that is its own inverse

In mathematics, an involution, involutory function, or self-inverse function is a function $f$ that is its own inverse,

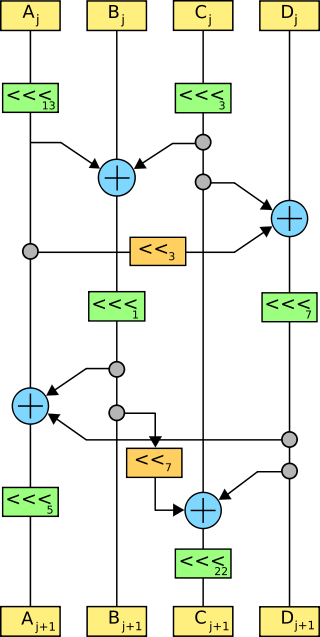
<span class="mw-page-title-main">Serpent (cipher)</span>

Serpent is a symmetric key block cipher that was a finalist in the Advanced Encryption Standard (AES) contest, where it was ranked second to Rijndael. Serpent was designed by Ross Anderson, Eli Biham, and Lars Knudsen.

In mathematics, the (field) norm is a particular mapping defined in field theory, which maps elements of a larger field into a subfield.

The affine cipher is a type of monoalphabetic substitution cipher, where each letter in an alphabet is mapped to its numeric equivalent, encrypted using a simple mathematical function, and converted back to a letter. The formula used means that each letter encrypts to one other letter, and back again, meaning the cipher is essentially a standard substitution cipher with a rule governing which letter goes to which. As such, it has the weaknesses of all substitution ciphers. Each letter is enciphered with the function $(ax + b) mod 26$ , where $b$ is the magnitude of the shift.

In linear algebra and functional analysis, a projection is a linear transformation $from a vector space to itself such that . That is, whenever is applied twice to any vector, it gives the same result as if it were applied once. It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.$

In mathematics, finite field arithmetic is arithmetic in a finite field contrary to arithmetic in a field with an infinite number of elements, like the field of rational numbers.

AES uses a key schedule to expand a short key into a number of separate round keys. The three AES variants have a different number of rounds. Each variant requires a separate 128-bit round key for each round plus one more. The key schedule produces the needed round keys from the initial key.

The MixColumns operation performed by the Rijndael cipher, along with the ShiftRows step, is the primary source of diffusion in Rijndael. Each column is treated as a four-term polynomial $which are elements within the field . The coefficients of the polynomials are elements within the prime sub-field .$

In mathematics and theoretical physics, the Berezinian or superdeterminant is a generalization of the determinant to the case of supermatrices. The name is for Felix Berezin. The Berezinian plays a role analogous to the determinant when considering coordinate changes for integration on a supermanifold.

ShāngMì 4 is a block cipher used in the Chinese National Standard for Wireless LAN WAPI and also used with Transport Layer Security.

In cryptography, M8 is a block cipher designed by Hitachi in 1999. It is a modification of Hitachi's earlier M6 algorithm, designed for greater security and high performance in both hardware and 32-bit software implementations. M8 was registered by Hitachi in March 1999 as ISO/IEC 9979-0020.

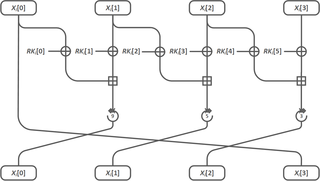
The Lightweight Encryption Algorithm is a 128-bit block cipher developed by South Korea in 2013 to provide confidentiality in high-speed environments such as big data and cloud computing, as well as lightweight environments such as IoT devices and mobile devices. LEA has three different key lengths: 128, 192, and 256 bits. LEA encrypts data about 1.5 to 2 times faster than AES, the most widely used block cipher in various software environments.

References

1 2 "The Rijndael Block Cipher" (PDF). Retrieved 2013-11-11.
↑ Nyberg K. (1991) Perfect nonlinear S-boxes. In: Davies D.W. (eds) Advances in Cryptology — EUROCRYPT ’91. EUROCRYPT 1991. Lecture Notes in Computer Science, vol 547. Springer, Berlin, Heidelberg
↑ "The Advanced Encryption Standard" (PDF). FIPS PUB 197: the official AES standard. Federal Information Processing Standard. 2001-11-26. Retrieved 2010-04-29.
↑ Jörg J. Buchholz (2001-12-19). "Matlab implementation of the Advanced Encryption Standard" (PDF).
↑ Jie Cui; Liusheng Huang; Hong Zhong; Chinchen Chang; Wei Yang (May 2011). "An Improved AES S-box and Its Performance Analysis" (PDF).

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[rijndael_cipher-1] 1 2 "The Rijndael Block Cipher" (PDF). Retrieved 2013-11-11.

[2] Nyberg K. (1991) Perfect nonlinear S-boxes. In: Davies D.W. (eds) Advances in Cryptology — EUROCRYPT ’91. EUROCRYPT 1991. Lecture Notes in Computer Science, vol 547. Springer, Berlin, Heidelberg

[fips197-3] "The Advanced Encryption Standard" (PDF). FIPS PUB 197: the official AES standard. Federal Information Processing Standard. 2001-11-26. Retrieved 2010-04-29.

[4] Jörg J. Buchholz (2001-12-19). "Matlab implementation of the Advanced Encryption Standard" (PDF).

[5] Jie Cui; Liusheng Huang; Hong Zhong; Chinchen Chang; Wei Yang (May 2011). "An Improved AES S-box and Its Performance Analysis" (PDF).

[1]

[2]

[3]

[4]

[5]

	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
00	52	09	6a	d5	30	36	a5	38	bf	40	a3	9e	81	f3	d7	fb
10	7c	e3	39	82	9b	2f	ff	87	34	8e	43	44	c4	de	e9	cb
20	54	7b	94	32	a6	c2	23	3d	ee	4c	95	0b	42	fa	c3	4e
30	08	2e	a1	66	28	d9	24	b2	76	5b	a2	49	6d	8b	d1	25
40	72	f8	f6	64	86	68	98	16	d4	a4	5c	cc	5d	65	b6	92
50	6c	70	48	50	fd	ed	b9	da	5e	15	46	57	a7	8d	9d	84
60	90	d8	ab	00	8c	bc	d3	0a	f7	e4	58	05	b8	b3	45	06
70	d0	2c	1e	8f	ca	3f	0f	02	c1	af	bd	03	01	13	8a	6b
80	3a	91	11	41	4f	67	dc	ea	97	f2	cf	ce	f0	b4	e6	73
90	96	ac	74	22	e7	ad	35	85	e2	f9	37	e8	1c	75	df	6e
a0	47	f1	1a	71	1d	29	c5	89	6f	b7	62	0e	aa	18	be	1b
b0	fc	56	3e	4b	c6	d2	79	20	9a	db	c0	fe	78	cd	5a	f4
c0	1f	dd	a8	33	88	07	c7	31	b1	12	10	59	27	80	ec	5f
d0	60	51	7f	a9	19	b5	4a	0d	2d	e5	7a	9f	93	c9	9c	ef
e0	a0	e0	3b	4d	ae	2a	f5	b0	c8	eb	bb	3c	83	53	99	61
f0	17	2b	04	7e	ba	77	d6	26	e1	69	14	63	55	21	0c	7d

	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
00	52	09	6a	d5	30	36	a5	38	bf	40	a3	9e	81	f3	d7	fb
10	7c	e3	39	82	9b	2f	ff	87	34	8e	43	44	c4	de	e9	cb
20	54	7b	94	32	a6	c2	23	3d	ee	4c	95	0b	42	fa	c3	4e
30	08	2e	a1	66	28	d9	24	b2	76	5b	a2	49	6d	8b	d1	25
40	72	f8	f6	64	86	68	98	16	d4	a4	5c	cc	5d	65	b6	92
50	6c	70	48	50	fd	ed	b9	da	5e	15	46	57	a7	8d	9d	84
60	90	d8	ab	00	8c	bc	d3	0a	f7	e4	58	05	b8	b3	45	06
70	d0	2c	1e	8f	ca	3f	0f	02	c1	af	bd	03	01	13	8a	6b
80	3a	91	11	41	4f	67	dc	ea	97	f2	cf	ce	f0	b4	e6	73
90	96	ac	74	22	e7	ad	35	85	e2	f9	37	e8	1c	75	df	6e
a0	47	f1	1a	71	1d	29	c5	89	6f	b7	62	0e	aa	18	be	1b
b0	fc	56	3e	4b	c6	d2	79	20	9a	db	c0	fe	78	cd	5a	f4
c0	1f	dd	a8	33	88	07	c7	31	b1	12	10	59	27	80	ec	5f
d0	60	51	7f	a9	19	b5	4a	0d	2d	e5	7a	9f	93	c9	9c	ef
e0	a0	e0	3b	4d	ae	2a	f5	b0	c8	eb	bb	3c	83	53	99	61
f0	17	2b	04	7e	ba	77	d6	26	e1	69	14	63	55	21	0c	7d