In computer science, an array is a data structure consisting of a collection of elements, of same memory size, each identified by at least one array index or key. An array is stored such that the position of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called one-dimensional array.
In mathematics, the determinant is a scalar value that is a certain function of the entries of a square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the linear map represented, on a given basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the corresponding linear map is an isomorphism. The determinant of a product of matrices is the product of their determinants.

In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex-valued function of frequency. The interval at which the DTFT is sampled is the reciprocal of the duration of the input sequence. An inverse DFT (IDFT) is a Fourier series, using the DTFT samples as coefficients of complex sinusoids at the corresponding DTFT frequencies. It has the same sample-values as the original input sequence. The DFT is therefore said to be a frequency domain representation of the original input sequence. If the original sequence spans all the non-zero values of a function, its DTFT is continuous, and the DFT provides discrete samples of one cycle. If the original sequence is one cycle of a periodic function, the DFT provides all the non-zero values of one DTFT cycle.

In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix.
In linear algebra, the outer product of two coordinate vectors is the matrix whose entries are all products of an element in the first vector with an element in the second vector. If the two coordinate vectors have dimensions n and m, then their outer product is an n × m matrix. More generally, given two tensors, their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.
In linear algebra, a square matrix is called diagonalizable or non-defective if it is similar to a diagonal matrix. That is, if there exists an invertible matrix and a diagonal matrix such that . This is equivalent to . This property exists for any linear map: for a finite-dimensional vector space , a linear map is called diagonalizable if there exists an ordered basis of consisting of eigenvectors of . These definitions are equivalent: if has a matrix representation as above, then the column vectors of form a basis consisting of eigenvectors of , and the diagonal entries of are the corresponding eigenvalues of ; with respect to this eigenvector basis, is represented by .
In mathematics and computer programming, index notation is used to specify the elements of an array of numbers. The formalism of how indices are used varies according to the subject. In particular, there are different methods for referring to the elements of a list, a vector, or a matrix, depending on whether one is writing a formal mathematical paper for publication, or when one is writing a computer program.

In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements is sometimes referred to as the sparsity of the matrix.
In computer programming, array slicing is an operation that extracts a subset of elements from an array and packages them as another array, possibly in a different dimension from the original.
In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers that describes the vector in terms of a particular ordered basis. An easy example may be a position such as in a 3-dimensional Cartesian coordinate system with the basis as the axes of this system. Coordinates are always specified relative to an ordered basis. Bases and their associated coordinate representations let one realize vector spaces and linear transformations concretely as column vectors, row vectors, and matrices; hence, they are useful in calculations.
In computer science, array programming refers to solutions that allow the application of operations to an entire set of values at once. Such solutions are commonly used in scientific and engineering settings.

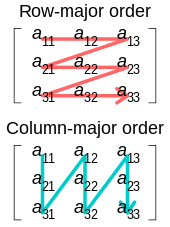
Matrix representation is a method used by a computer language to store column-vector matrices of more than one dimension in memory. Fortran and C use different schemes for their native arrays. Fortran uses "Column Major" (AoS), in which all the elements for a given column are stored contiguously in memory. C uses "Row Major" (SoA), which stores all the elements for a given row contiguously in memory. LAPACK defines various matrix representations in memory. There is also Sparse matrix representation and Morton-order matrix representation. According to the documentation, in LAPACK the unitary matrix representation is optimized. Some languages such as Java store matrices using Iliffe vectors. These are particularly useful for storing irregular matrices. Matrices are of primary importance in linear algebra.
In computer programming, an Iliffe vector, also known as a display, is a data structure used to implement multi-dimensional arrays.
In numerical analysis and linear algebra, lower–upper (LU) decomposition or factorization factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. LU decomposition can be viewed as the matrix form of Gaussian elimination. Computers usually solve square systems of linear equations using LU decomposition, and it is also a key step when inverting a matrix or computing the determinant of a matrix. The LU decomposition was introduced by the Polish astronomer Tadeusz Banachiewicz in 1938. To quote: "It appears that Gauss and Doolittle applied the method [of elimination] only to symmetric equations. More recent authors, for example, Aitken, Banachiewicz, Dwyer, and Crout … have emphasized the use of the method, or variations of it, in connection with non-symmetric problems … Banachiewicz … saw the point … that the basic problem is really one of matrix factorization, or “decomposition” as he called it." It is also sometimes referred to as LR decomposition.
In mathematics, especially in linear algebra and matrix theory, the commutation matrix is used for transforming the vectorized form of a matrix into the vectorized form of its transpose. Specifically, the commutation matrix K(m,n) is the nm × mn matrix which, for any m × n matrix A, transforms vec(A) into vec(AT):

In mathematics, a matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or property of such an object.
In computer science, array is a data type that represents a collection of elements, each selected by one or more indices that can be computed at run time during program execution. Such a collection is usually called an array variable or array value. By analogy with the mathematical concepts vector and matrix, array types with one and two indices are often called vector type and matrix type, respectively. More generally, a multidimensional array type can be called a tensor type, by analogy with the physical concept, tensor.
In signal processing, nonlinear multidimensional signal processing (NMSP) covers all signal processing using nonlinear multidimensional signals and systems. Nonlinear multidimensional signal processing is a subset of signal processing (multidimensional signal processing). Nonlinear multi-dimensional systems can be used in a broad range such as imaging, teletraffic, communications, hydrology, geology, and economics. Nonlinear systems cannot be treated as linear systems, using Fourier transformation and wavelet analysis. Nonlinear systems will have chaotic behavior, limit cycle, steady state, bifurcation, multi-stability and so on. Nonlinear systems do not have a canonical representation, like impulse response for linear systems. But there are some efforts to characterize nonlinear systems, such as Volterra and Wiener series using polynomial integrals as the use of those methods naturally extend the signal into multi-dimensions. Another example is the Empirical mode decomposition method using Hilbert transform instead of Fourier Transform for nonlinear multi-dimensional systems. This method is an empirical method and can be directly applied to data sets. Multi-dimensional nonlinear filters (MDNF) are also an important part of NMSP, MDNF are mainly used to filter noise in real data. There are nonlinear-type hybrid filters used in color image processing, nonlinear edge-preserving filters use in magnetic resonance image restoration. Those filters use both temporal and spatial information and combine the maximum likelihood estimate with the spatial smoothing algorithm.
In signal processing, multidimensional empirical mode decomposition is an extension of the one-dimensional (1-D) EMD algorithm to a signal encompassing multiple dimensions. The Hilbert–Huang empirical mode decomposition (EMD) process decomposes a signal into intrinsic mode functions combined with the Hilbert spectral analysis, known as the Hilbert–Huang transform (HHT). The multidimensional EMD extends the 1-D EMD algorithm into multiple-dimensional signals. This decomposition can be applied to image processing, audio signal processing, and various other multidimensional signals.