
In physics, optical depth or optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power through a material. Thus, the larger the optical depth, the smaller the amount of transmitted radiant power through the material. Spectral optical depth or spectral optical thickness is the natural logarithm of the ratio of incident to transmitted spectral radiant power through a material. Optical depth is dimensionless, and in particular is not a length, though it is a monotonically increasing function of optical path length, and approaches zero as the path length approaches zero. The use of the term "optical density" for optical depth is discouraged.
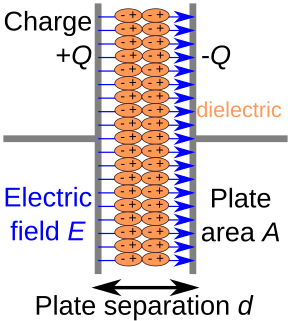
In electromagnetism, a dielectric is an electrical insulator that can be polarised by an applied electric field. When a dielectric material is placed in an electric field, electric charges do not flow through the material as they do in an electrical conductor, because they have no loosely bound, or free, electrons that may drift through the material, but instead they shift, only slightly, from their average equilibrium positions, causing dielectric polarisation. Because of dielectric polarisation, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field. This creates an internal electric field that reduces the overall field within the dielectric itself. If a dielectric is composed of weakly bonded molecules, those molecules not only become polarised, but also reorient so that their symmetry axes align to the field.

In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ε (epsilon), is a measure of the electric polarizability of a dielectric. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.

Thermal radiation is electromagnetic radiation generated by the thermal motion of particles in matter. Thermal radiation is generated when heat from the movement of charges in the material is converted to electromagnetic radiation. All matter with a temperature greater than absolute zero emits thermal radiation. At room temperature, most of the emission is in the infrared (IR) spectrum. Particle motion results in charge-acceleration or dipole oscillation which produces electromagnetic radiation.
The laser diode rate equations model the electrical and optical performance of a laser diode. This system of ordinary differential equations relates the number or density of photons and charge carriers (electrons) in the device to the injection current and to device and material parameters such as carrier lifetime, photon lifetime, and the optical gain.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.

Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is the low-energy limit of Compton scattering: the particle's kinetic energy and photon frequency do not change as a result of the scattering. This limit is valid as long as the photon energy is much smaller than the mass energy of the particle: , or equivalently, if the wavelength of the light is much greater than the Compton wavelength of the particle.
The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:
Non-line-of-sight (NLOS) radio propagation occurs outside of the typical line-of-sight (LOS) between the transmitter and receiver, such as in ground reflections. Near-line-of-sight conditions refer to partial obstruction by a physical object present in the innermost Fresnel zone.
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.

Kenneth Stewart Cole was an American biophysicist described by his peers as "a pioneer in the application of physical science to biology". Cole was awarded the National Medal of Science in 1967.
The surface of the Sun radiates light and heat at approximately 5,500 °C. The Earth is much cooler and so radiates heat back away from itself at much longer wavelengths, mostly in the infrared range. The idealized greenhouse model is based on the fact that certain gases in the Earth's atmosphere, including carbon dioxide and water vapour, are transparent to the high-frequency, high-energy solar radiation, but are much more opaque to the lower frequency infrared radiation leaving the surface of the earth. Thus heat is easily let in, but is partially trapped by these gases as it tries to leave. Rather than get hotter and hotter, Kirchhoff's law of thermal radiation says that the gases of the atmosphere also have to re-emit the infrared energy that they absorb, and they do so, also at long infrared wavelengths, both upwards into space as well as downwards back towards the Earth's surface. In the long-term, thermal equilibrium is reached when all the heat energy arriving on the planet is leaving again at the same rate. In this idealized model, the greenhouse gases cause the surface of the planet to be warmer than it would be without them, in order for the required amount of heat energy finally to be radiated out into space from the top of the atmosphere.
The Stoner criterion is a condition to be fulfilled for the ferromagnetic order to arise in a simplified model of a solid. It is named after Edmund Clifton Stoner.

A microwave cavity or radio frequency (RF) cavity is a special type of resonator, consisting of a closed metal structure that confines electromagnetic fields in the microwave region of the spectrum. The structure is either hollow or filled with dielectric material. The microwaves bounce back and forth between the walls of the cavity. At the cavity's resonant frequencies they reinforce to form standing waves in the cavity. Therefore, the cavity functions similarly to an organ pipe or sound box in a musical instrument, oscillating preferentially at a series of frequencies, its resonant frequencies. Thus it can act as a bandpass filter, allowing microwaves of a particular frequency to pass while blocking microwaves at nearby frequencies.
In dielectric spectroscopy, large frequency dependent contributions to the dielectric response, especially at low frequencies, may come from build-ups of charge. This Maxwell–Wagner–Sillars polarization, occurs either at inner dielectric boundary layers on a mesoscopic scale, or at the external electrode-sample interface on a macroscopic scale. In both cases this leads to a separation of charges. The charges are often separated over a considerable distance, and the contribution to dielectric loss can therefore be orders of magnitude larger than the dielectric response due to molecular fluctuations.
Ultrasound-modulated optical tomography (UOT) is a form of tomography involving ultrasound. It is used in imaging of biological soft tissues and has potential applications for early cancer detection. Like optical techniques, this method provides high contrast, and the use of ultrasound also provides high resolution.
The Grey atmosphere is a useful set of approximations made for radiative transfer applications in studies of stellar atmospheres based on the simplified notion that the absorption coefficient of matter within a star's atmosphere is constant—that is, unchanging—for all frequencies of the star's incident radiation.

Semiconductor lasers or laser diodes play an important part in our everyday lives by providing cheap and compact-size lasers. They consist of complex multi-layer structures requiring nanometer scale accuracy and an elaborate design. Their theoretical description is important not only from a fundamental point of view, but also in order to generate new and improved designs. It is common to all systems that the laser is an inverted carrier density system. The carrier inversion results in an electromagnetic polarization which drives an electric field . In most cases, the electric field is confined in a resonator, the properties of which are also important factors for laser performance.
Satellite surface salinity refers to measurements of surface salinity made by remote sensing satellites. The radiative properties of the ocean surface are exploited in order to estimate the salinity of the water's surface layer.
The Cole-Davidson equation is a model used to describe dielectric relaxation in glass-forming liquids. The equation for the complex permittivity is



























