
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function f is a differentiable function F whose derivative is equal to the original function f. This can be stated symbolically as F' = f. The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as F and G.
In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets. Some authors require additional restrictions on the measure, as described below.

In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers is not compact either, because it excludes the two limiting values and . However, the extended real number linewould be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces.

In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter (aleph) marked with subscript indicating their rank among the infinite cardinals.

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".

In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter.

In mathematical analysis, a null set is a Lebesgue measurable set of real numbers that has measure zero. This can be characterized as a set that can be covered by a countable union of intervals of arbitrarily small total length.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
In mathematics, a (real) interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. An interval can contain neither endpoint, either endpoint, or both endpoints.
In mathematical analysis, Fubini's theorem is a result that gives conditions under which it is possible to compute a double integral by using an iterated integral, introduced by Guido Fubini in 1907. One may switch the order of integration if the double integral yields a finite answer when the integrand is replaced by its absolute value.
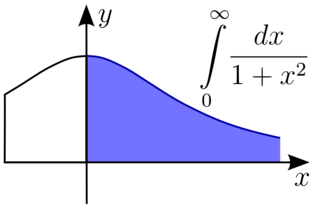
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.
In mathematics, two sets are almost disjoint if their intersection is small in some sense; different definitions of "small" will result in different definitions of "almost disjoint".
Lutz's resource-bounded measure is a generalisation of Lebesgue measure to complexity classes. It was originally developed by Jack Lutz. Just as Lebesgue measure gives a method to quantify the size of subsets of the Euclidean space , resource bounded measure gives a method to classify the size of subsets of complexity classes.
In measure theory, Carathéodory's extension theorem states that any pre-measure defined on a given ring of subsets R of a given set Ω can be extended to a measure on the σ-ring generated by R, and this extension is unique if the pre-measure is σ-finite. Consequently, any pre-measure on a ring containing all intervals of real numbers can be extended to the Borel algebra of the set of real numbers. This is an extremely powerful result of measure theory, and leads, for example, to the Lebesgue measure.
In mathematics, a positive (or signed) measure μ defined on a σ-algebra Σ of subsets of a set X is called a finite measure if μ(X) is a finite real number (rather than ∞). A set A in Σ is of finite measure if μ(A) < ∞. The measure μ is called σ-finite if X is a countable union of measurable sets each with finite measure. A set in a measure space is said to have σ-finite measure if it is a countable union of measurable sets with finite measure. A measure being σ-finite is a weaker condition than being finite, i.e. all finite measures are σ-finite but there are (many) σ-finite measures that are not finite.
In mathematics, in particular in measure theory, a content is a real-valued function defined on a collection of subsets such that

Infinity is something which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .

In mathematics, Hilbert spaces allow the methods of linear algebra and calculus to be generalized from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that induces a distance function for which the space is a complete metric space.

In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the X axis. The Lebesgue integral, named after French mathematician Henri Lebesgue, extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.













