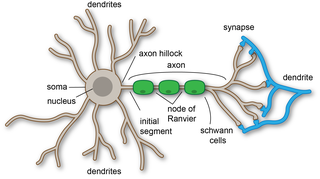
A dendrite or dendron is a branched protoplasmic extension of a nerve cell that propagates the electrochemical stimulation received from other neural cells to the cell body, or soma, of the neuron from which the dendrites project. Electrical stimulation is transmitted onto dendrites by upstream neurons via synapses which are located at various points throughout the dendritic tree.

Within a nervous system, a neuron, neurone, or nerve cell is an electrically excitable cell that fires electric signals called action potentials across a neural network. Neurons communicate with other cells via synapses, which are specialized connections that commonly use minute amounts of chemical neurotransmitters to pass the electric signal from the presynaptic neuron to the target cell through the synaptic gap.

A dendritic spine is a small membranous protrusion from a neuron's dendrite that typically receives input from a single axon at the synapse. Dendritic spines serve as a storage site for synaptic strength and help transmit electrical signals to the neuron's cell body. Most spines have a bulbous head, and a thin neck that connects the head of the spine to the shaft of the dendrite. The dendrites of a single neuron can contain hundreds to thousands of spines. In addition to spines providing an anatomical substrate for memory storage and synaptic transmission, they may also serve to increase the number of possible contacts between neurons. It has also been suggested that changes in the activity of neurons have a positive effect on spine morphology.

An artificial neuron is a mathematical function conceived as a model of biological neurons in a neural network. Artificial neurons are the elementary units of artificial neural networks. The artificial neuron is a function that receives one or more inputs, applies weights to these inputs, and sums them to produce an output.

Pyramidal cells, or pyramidal neurons, are a type of multipolar neuron found in areas of the brain including the cerebral cortex, the hippocampus, and the amygdala. Pyramidal cells are the primary excitation units of the mammalian prefrontal cortex and the corticospinal tract. One of the main structural features of the pyramidal neuron is the conic shaped soma, or cell body, after which the neuron is named. Other key structural features of the pyramidal cell are a single axon, a large apical dendrite, multiple basal dendrites, and the presence of dendritic spines.

In cellular neuroscience, the soma, perikaryon, neurocyton, or cell body is the bulbous, non-process portion of a neuron or other brain cell type, containing the cell nucleus. Although it is often used to refer to neurons, it can also refer to other cell types as well, including astrocytes, oligodendrocytes, and microglia. There are many different specialized types of neurons, and their sizes vary from as small as about 5 micrometres to over 10 millimetres for some of the smallest and largest neurons of invertebrates, respectively.
An apical dendrite is a dendrite that emerges from the apex of a pyramidal cell. Apical dendrites are one of two primary categories of dendrites, and they distinguish the pyramidal cells from spiny stellate cells in the cortices. Pyramidal cells are found in the prefrontal cortex, the hippocampus, the entorhinal cortex, the olfactory cortex, and other areas. Dendrite arbors formed by apical dendrites are the means by which synaptic inputs into a cell are integrated. The apical dendrites in these regions contribute significantly to memory, learning, and sensory associations by modulating the excitatory and inhibitory signals received by the pyramidal cells.

In neuroscience, Golgi cells are the most abundant inhibitory interneurons found within the granular layer of the cerebellum. Golgi cells can be found in the granular layer at various layers. The Golgi cell is essential for controlling the activity of the granular layer. They were first identified as inhibitory in 1964. It was also the first example of an inhibitory feedback network in which the inhibitory interneuron was identified anatomically. Golgi cells produce a wide lateral inhibition that reaches beyond the afferent synaptic field and inhibit granule cells via feedforward and feedback inhibitory loops. These cells synapse onto the dendrite of granule cells and unipolar brush cells. They receive excitatory input from mossy fibres, also synapsing on granule cells, and parallel fibers, which are long granule cell axons. Thereby this circuitry allows for feed-forward and feed-back inhibition of granule cells.
NeuronStudio was a non-commercial program created at Icahn School of Medicine at Mount Sinai by the Computational Neurobiology and Imaging Center. This program performed automatic tracing and reconstruction of neuron structures from confocal image stacks. The resulting models were then exported to file using standard formats for further processing, modeling, or for statistical analyses. NeuronStudio handled morphologic details on scales spanning local Dendritic spine geometry through complex tree topology to the gross spatial arrangement of multi-neuron networks. Its capability for automated digitization avoided the subjective errors inherent in manual tracing. The program ceased to be supported in 2012 and the project pages were eventually removed from the ISMMS Website. Its documentation and the Windows source code however are still available via the Internet Archive.
A neurite or neuronal process refers to any projection from the cell body of a neuron. This projection can be either an axon or a dendrite. The term is frequently used when speaking of immature or developing neurons, especially of cells in culture, because it can be difficult to tell axons from dendrites before differentiation is complete.

In neuroscience, classical cable theory uses mathematical models to calculate the electric current along passive neurites, particularly the dendrites that receive synaptic inputs at different sites and times. Estimates are made by modeling dendrites and axons as cylinders composed of segments with capacitances and resistances combined in parallel. The capacitance of a neuronal fiber comes about because electrostatic forces are acting through the very thin lipid bilayer. The resistance in series along the fiber is due to the axoplasm's significant resistance to movement of electric charge.
Neuromorphology is the study of nervous system form, shape, and structure. The study involves looking at a particular part of the nervous system from a molecular and cellular level and connecting it to a physiological and anatomical point of view. The field also explores the communications and interactions within and between each specialized section of the nervous system. Morphology is distinct from morphogenesis. Morphology is the study of the shape and structure of biological organisms, while morphogenesis is the study of the biological development of the shape and structure of organisms. Therefore, neuromorphology focuses on the specifics of the structure of the nervous system and not the process by which the structure was developed. Neuromorphology and morphogenesis, while two different entities, are nonetheless closely linked.
The synaptotropic hypothesis, also called the synaptotrophic hypothesis, is a neurobiological hypothesis of neuronal growth and synapse formation. The hypothesis was first formulated by J.E. Vaughn in 1988, and remains a focus of current research efforts. The synaptotropic hypothesis proposes that input from a presynaptic to a postsynaptic cell eventually can change the course of synapse formation at dendritic and axonal arbors. This synapse formation is required for the development of neuronal structure in the functioning brain.
Neural backpropagation is the phenomenon in which, after the action potential of a neuron creates a voltage spike down the axon, another impulse is generated from the soma and propagates towards the apical portions of the dendritic arbor or dendrites. In addition to active backpropagation of the action potential, there is also passive electrotonic spread. While there is ample evidence to prove the existence of backpropagating action potentials, the function of such action potentials and the extent to which they invade the most distal dendrites remain highly controversial.

Biological neuron models, also known as spiking neuron models, are mathematical descriptions of the conduction of electrical signals in neurons. Neurons are electrically excitable cells within the nervous system, able to fire electric signals, called action potentials, across a neural network. These mathematical models describe the role of the biophysical and geometrical characteristics of neurons on the conduction of electrical activity.

In neurophysiology, a dendritic spike refers to an action potential generated in the dendrite of a neuron. Dendrites are branched extensions of a neuron. They receive electrical signals emitted from projecting neurons and transfer these signals to the cell body, or soma. Dendritic signaling has traditionally been viewed as a passive mode of electrical signaling. Unlike its axon counterpart which can generate signals through action potentials, dendrites were believed to only have the ability to propagate electrical signals by physical means: changes in conductance, length, cross sectional area, etc. However, the existence of dendritic spikes was proposed and demonstrated by W. Alden Spencer, Eric Kandel, Rodolfo Llinás and coworkers in the 1960s and a large body of evidence now makes it clear that dendrites are active neuronal structures. Dendrites contain voltage-gated ion channels giving them the ability to generate action potentials. Dendritic spikes have been recorded in numerous types of neurons in the brain and are thought to have great implications in neuronal communication, memory, and learning. They are one of the major factors in long-term potentiation.
Compartmental modelling of dendrites deals with multi-compartment modelling of the dendrites, to make the understanding of the electrical behavior of complex dendrites easier. Basically, compartmental modelling of dendrites is a very helpful tool to develop new biological neuron models. Dendrites are very important because they occupy the most membrane area in many of the neurons and give the neuron an ability to connect to thousands of other cells. Originally the dendrites were thought to have constant conductance and current but now it has been understood that they may have active Voltage-gated ion channels, which influences the firing properties of the neuron and also the response of neuron to synaptic inputs. Many mathematical models have been developed to understand the electric behavior of the dendrites. Dendrites tend to be very branchy and complex, so the compartmental approach to understand the electrical behavior of the dendrites makes it very useful.
Neuronal tracing, or neuron reconstruction is a technique used in neuroscience to determine the pathway of the neurites or neuronal processes, the axons and dendrites, of a neuron. From a sample preparation point of view, it may refer to some of the following as well as other genetic neuron labeling techniques,

Neuronal self-avoidance, or isoneural avoidance, is an important property of neurons which consists in the tendency of branches arising from a single soma to turn away from one another. The arrangements of branches within neuronal arbors are established during development and result in minimal crossing or overlap as they spread over a territory, resulting in the typical fasciculated morphology of neurons.
Patch-sequencing (patch-seq) is a modification of patch-clamp technique that combines electrophysiological, transcriptomic and morphological characterization of individual neurons. In this approach, the neuron's cytoplasm is collected and processed for RNAseq after electrophysiological recordings are performed on it. The cell is simultaneously filled with a dye that allows for subsequent morphological reconstruction.















