
A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support variable length output. The values returned by a hash function are called hash values, hash codes, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter storage addressing.

In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an index, also called a hash code, into an array of buckets or slots, from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.
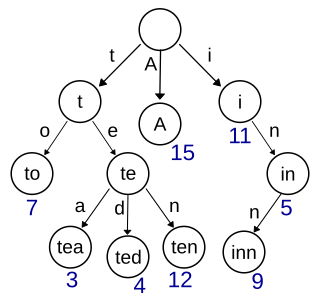
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

A distributed hash table (DHT) is a distributed system that provides a lookup service similar to a hash table. Key–value pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key. The main advantage of a DHT is that nodes can be added or removed with minimum work around re-distributing keys. Keys are unique identifiers which map to particular values, which in turn can be anything from addresses, to documents, to arbitrary data. Responsibility for maintaining the mapping from keys to values is distributed among the nodes, in such a way that a change in the set of participants causes a minimal amount of disruption. This allows a DHT to scale to extremely large numbers of nodes and to handle continual node arrivals, departures, and failures.

A longest common subsequence (LCS) is the longest subsequence common to all sequences in a set of sequences. It differs from the longest common substring: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. The problem of computing longest common subsequences is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in computational linguistics and bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files.

In computer science, a perfect hash functionh for a set S is a hash function that maps distinct elements in S to a set of m integers, with no collisions. In mathematical terms, it is an injective function.
Kademlia is a distributed hash table for decentralized peer-to-peer computer networks designed by Petar Maymounkov and David Mazières in 2002. It specifies the structure of the network and the exchange of information through node lookups. Kademlia nodes communicate among themselves using UDP. A virtual or overlay network is formed by the participant nodes. Each node is identified by a number or node ID. The node ID serves not only as identification, but the Kademlia algorithm uses the node ID to locate values.
A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set. False positive matches are possible, but false negatives are not – in other words, a query returns either "possibly in set" or "definitely not in set". Elements can be added to the set, but not removed ; the more items added, the larger the probability of false positives.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.

Linear probing is a scheme in computer programming for resolving collisions in hash tables, data structures for maintaining a collection of key–value pairs and looking up the value associated with a given key. It was invented in 1954 by Gene Amdahl, Elaine M. McGraw, and Arthur Samuel and first analyzed in 1963 by Donald Knuth.
In computer science, consistent hashing is a special kind of hashing technique such that when a hash table is resized, only keys need to be remapped on average where is the number of keys and is the number of slots. In contrast, in most traditional hash tables, a change in the number of array slots causes nearly all keys to be remapped because the mapping between the keys and the slots is defined by a modular operation.
Linear hashing (LH) is a dynamic data structure which implements a hash table and grows or shrinks one bucket at a time. It was invented by Witold Litwin in 1980. It has been analyzed by Baeza-Yates and Soza-Pollman. It is the first in a number of schemes known as dynamic hashing such as Larson's Linear Hashing with Partial Extensions, Linear Hashing with Priority Splitting, Linear Hashing with Partial Expansions and Priority Splitting, or Recursive Linear Hashing.

Cuckoo hashing is a scheme in computer programming for resolving hash collisions of values of hash functions in a table, with worst-case constant lookup time. The name derives from the behavior of some species of cuckoo, where the cuckoo chick pushes the other eggs or young out of the nest when it hatches in a variation of the behavior referred to as brood parasitism; analogously, inserting a new key into a cuckoo hashing table may push an older key to a different location in the table.
Extendible hashing is a type of hash system which treats a hash as a bit string and uses a trie for bucket lookup. Because of the hierarchical nature of the system, re-hashing is an incremental operation. This means that time-sensitive applications are less affected by table growth than by standard full-table rehashes.
In computer science, a succinct data structure is a data structure which uses an amount of space that is "close" to the information-theoretic lower bound, but still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees, and planar graphs. Unlike general lossless data compression algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure, insofar as the size of the stored or encoded data similarly depends upon the specific content of the data itself.
In computer science, locality-sensitive hashing (LSH) is an algorithmic technique that hashes similar input items into the same "buckets" with high probability. Since similar items end up in the same buckets, this technique can be used for data clustering and nearest neighbor search. It differs from conventional hashing techniques in that hash collisions are maximized, not minimized. Alternatively, the technique can be seen as a way to reduce the dimensionality of high-dimensional data; high-dimensional input items can be reduced to low-dimensional versions while preserving relative distances between items.
In computer science, streaming algorithms are algorithms for processing data streams in which the input is presented as a sequence of items and can be examined in only a few passes, typically just one. These algorithms are designed to operate with limited memory, generally logarithmic in the size of the stream and/or in the maximum value in the stream, and may also have limited processing time per item.
In computer science, dynamic perfect hashing is a programming technique for resolving collisions in a hash table data structure. While more memory-intensive than its hash table counterparts, this technique is useful for situations where fast queries, insertions, and deletions must be made on a large set of elements.

A bucket queue is a data structure that implements the priority queue abstract data type: it maintains a dynamic collection of elements with numerical priorities and allows quick access to the element with minimum priority. In the bucket queue, the priorities must be integers, and it is particularly suited to applications in which the priorities have a small range. A bucket queue has the form of an array of buckets: an array data structure, indexed by the priorities, whose cells contain collections of items with the same priority as each other. With this data structure, insertion of elements and changes of their priority take constant time. Searching for and removing the minimum-priority element takes time proportional to the number of buckets or, by maintaining a pointer to the most recently found bucket, in time proportional to the difference in priorities between successive operations.

Searchable symmetric encryption (SSE) is a form of encryption that allows one to efficiently search over a collection of encrypted documents or files without the ability to decrypt them. SSE can be used to outsource files to an untrusted cloud storage server without ever revealing the files in the clear but while preserving the server's ability to search over them.















