Stars and bars (combinatorics)

Last updated May 17, 2024

In the context of combinatorial mathematics, stars and bars (also called "sticks and stones",^[1] "balls and bars",^[2] and "dots and dividers"^[3]) is a graphical aid for deriving certain combinatorial theorems. It can be used to solve many simple counting problems, such as how many ways there are to put $n$ indistinguishable balls into $k$ distinguishable bins.^[4]

Statements of theorems

The stars and bars method is often introduced specifically to prove the following two theorems of elementary combinatorics concerning the number of solutions to an equation.

Theorem one

For any pair of positive integers $n$ and $k$ , the number of $k$ -tuples of positive integers whose sum is $n$ is equal to the number of $(k - 1)$ -element subsets of a set with $n - 1$ elements.

For example, if $n = 10$ and $k = 4$ , the theorem gives the number of solutions to $x 1 + x 2 + x 3 + x 4 = 10$ (with $x 1, x 2, x 3, x 4 > 0$ ) as the binomial coefficient

{\binom {n-1}{k-1}}={\binom {10-1}{4-1}}={\binom {9}{3}}=84.

This corresponds to compositions of an integer.

Theorem two

For any pair of positive integers $n$ and $k$ , the number of $k$ -tuples of non-negative integers whose sum is $n$ is equal to the number of multisets of cardinality $n$ taken from a set of size $k$ , or equivalently, the number of multisets of cardinality $k - 1$ taken from a set of size $n + 1$ .

For example, if $n = 10$ and $k = 4$ , the theorem gives the number of solutions to $x 1 + x 2 + x 3 + x 4 = 10$ (with $\geq 0$ ) as:

\left(\!\!{k \choose n}\!\!\right)={k+n-1 \choose n}={\binom {13}{10}}=286

\left(\!\!{n+1 \choose k-1}\!\!\right)={n+1+k-1-1 \choose k-1}={\binom {13}{3}}=286

{\binom {n+k-1}{k-1}}={\binom {10+4-1}{4-1}}={\binom {13}{3}}=286

This corresponds to weak compositions of an integer.

Proofs via the method of stars and bars

Theorem one proof

Suppose there are n objects (represented here by stars) to be placed into k bins, such that all bins contain at least one object. The bins are distinguishable (say they are numbered 1 to k) but the n stars are not (so configurations are only distinguished by the number of stars present in each bin). A configuration is thus represented by a k-tuple of positive integers, as in the statement of the theorem.

For example, with $n = 7$ and $k = 3$ , start by placing the stars in a line:

★ ★ ★ ★ ★ ★ ★

Fig. 1: Seven objects, represented by stars

The configuration will be determined once it is known which is the first star going to the second bin, and the first star going to the third bin, etc.. This is indicated by placing $k - 1$ bars between the stars. Because no bin is allowed to be empty (all the variables are positive), there is at most one bar between any pair of stars.

For example:

★ ★ ★ ★ | ★ | ★ ★

Fig. 2: These two bars give rise to three bins containing 4, 1, and 2 objects

There are $n - 1$ gaps between stars. A configuration is obtained by choosing $k - 1$ of these gaps to contain a bar; therefore there are ${\tbinom {n-1}{k-1}}$ possible combinations.

Theorem two proof

In this case, the weakened restriction of non-negativity instead of positivity means that we can place multiple bars between stars, before the first star and after the last star.

For example, when $n = 7$ and $k = 5$ , the tuple (4, 0, 1, 2, 0) may be represented by the following diagram:

★ ★ ★ ★ || ★ | ★ ★ |

Fig. 3: These four bars give rise to five bins containing 4, 0, 1, 2, and 0 objects

To see that there are ${\tbinom {n+k-1}{k-1}}$ possible arrangements, observe that any arrangement of stars and bars consists of a total of $n + k - 1$ objects, n of which are stars and $k - 1$ of which are bars. Thus, we only need to choose $k - 1$ of the $n + k - 1$ positions to be bars (or, equivalently, choose n of the positions to be stars).

Theorem 1 can now be restated in terms of Theorem 2, because the requirement that all the variables are positive is equivalent to pre-assigning each variable a 1, and asking for the number of solutions when each variable is non-negative.

For example:

x_{1}+x_{2}+x_{3}+x_{4}=10

with $x_{1},x_{2},x_{3},x_{4}>0$

is equivalent to:

x_{1}+x_{2}+x_{3}+x_{4}=6

with $x_{1},x_{2},x_{3},x_{4}\geq 0$

Proofs by generating functions

Both cases are very similar, we will look at the case when $x_{i}\geq 0$ first. The 'bucket' becomes

{\frac {1}{1-x}}

This can also be written as

1+x+x^{2}+\dots

and the exponent of $x$ tells us how many balls are placed in the bucket.

Each additional bucket is represented by another ${\frac {1}{1-x}}$ , and so the final generating function is

{\frac {1}{1-x}}{\frac {1}{1-x}}\dots {\frac {1}{1-x}}={\frac {1}{(1-x)^{k}}}

As we only have $n$ balls, we want the coefficient of $x^{n}$ (written $[x^{n}]:$ ) from this

[x^{n}]:{\frac {1}{(1-x)^{k}}}

This is a well-known generating function - it generates the diagonals in Pascal's Triangle, and the coefficient of $x^{n}$ is

{\binom {n+k-1}{k-1}}

For the case when $x_{i}>0$ , we need to add $x$ into the numerator to indicate that at least one ball is in the bucket.

{\frac {x}{1-x}}{\frac {x}{1-x}}\dots {\frac {x}{1-x}}={\frac {x^{k}}{(1-x)^{k}}}

and the coefficient of $x^{n}$ is

{\binom {n-1}{k-1}}

Examples

Many elementary word problems in combinatorics are resolved by the theorems above.

Example 1

If one wishes to count the number of ways to distribute seven indistinguishable one dollar coins among Amber, Ben, and Curtis so that each of them receives at least one dollar, one may observe that distributions are essentially equivalent to tuples of three positive integers whose sum is 7. (Here the first entry in the tuple is the number of coins given to Amber, and so on.) Thus stars and bars theorem 1 applies, with $n = 7$ and $k = 3$ , and there are ${\tbinom {7-1}{3-1}}=15$ ways to distribute the coins.

Example 2

If $n = 5$ , $k = 4$ , and a set of size $k$ is ${a, b, c, d},$ then ★|★★★||★ could represent either the multiset ${a, b, b, b, d}$ or the 4-tuple $(1, 3, 0, 1).$ The representation of any multiset for this example should use SAB2 with $n = 5$ , $k - 1 = 3$ bars to give ${\tbinom {5+4-1}{4-1}}={\tbinom {8}{3}}=56$ .

Example 3

SAB2 allows for more bars than stars, which isn't permitted in SAB1.

So, for example, 10 balls into 7 bins is ${\tbinom {16}{6}}$ , while 7 balls into 10 bins is ${\tbinom {16}{9}}$ , with 6 balls into 11 bins as ${\tbinom {16}{10}}={\tbinom {16}{6}}.$

Example 4

If we have the infinite power series

\left[\sum _{k=1}^{\infty }x^{k}\right],

we can use this method to compute the Cauchy product of $m$ copies of the series. For the $n$ th term of the expansion, we are picking $n$ powers of $x$ from m separate locations. Hence there are ${\tbinom {n-1}{m-1}}$ ways to form our $n$ th power:

\left[\sum _{k=1}^{\infty }x^{k}\right]^{m}=\sum _{n=m}^{\infty }{{n-1} \choose {m-1}}x^{n}

Example 5

The graphical method was used by Paul Ehrenfest and Heike Kamerlingh Onnes—with symbol ε (quantum energy element) in place of a star and the symbol 0 in place of a bar—as a simple derivation of Max Planck's expression for the number of "complexions" for a system of "resonators" of a single frequency.^[5]^[6]

By complexions (microstates) Planck meant distributions of $P$ energy elements ε over $N$ resonators.^[7]^[8] The number $R$ of complexions is

R={\frac {(N+P-1)!}{P!(N-1)!}}.\

The graphical representation of each possible distribution would contain $P$ copies of the symbol ε and $N - 1$ copies of the symbol 0. In their demonstration, Ehrenfest and Kamerlingh Onnes took $N = 4$ and $P = 7$ (i.e., $R = 120$ combinations). They chose the 4-tuple (4, 2, 0, 1) as the illustrative example for this symbolic representation: εεεε0εε00ε.

Related Research Articles

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n; this coefficient can be computed by the multiplicative formula$

In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial $(x + y) n$ into a sum involving terms of the form $ax b y c$ , where the exponents $b$ and $c$ are nonnegative integers with $b + c = n$ , and the coefficient $a$ of each term is a specific positive integer depending on $n$ and $b$ . For example, for $n = 4$ ,

In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by $or, is equal to the binomial coefficient$

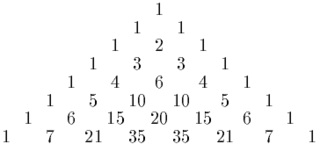
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.

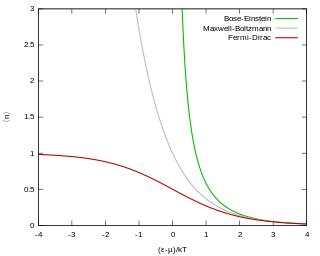
In quantum statistics, Bose–Einstein statistics describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles can be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose.

In mathematics, the falling factorial is defined as the polynomial

In mathematics, Bertrand's postulate states that, for each $, there is a prime such that . First conjectured in 1845 by Joseph Bertrand, it was first proven by Chebyshev, and a shorter but also advanced proof was given by Ramanujan.$

In mathematics, a multiset is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist which contain only elements $a$ and $b$ , but vary in the multiplicities of their elements:

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.

Multi-index notation is a mathematical notation that simplifies formulas used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices.

In mathematics, the binomial series is a generalization of the polynomial that comes from a binomial formula expression like $for a nonnegative integer . Specifically, the binomial series is the MacLaurin series for the function, where and . Explicitly,$

In combinatorics, Bertrand's ballot problem is the question: "In an election where candidate A receives p votes and candidate B receives q votes with p > q, what is the probability that A will be strictly ahead of B throughout the count?" The answer is

In mathematics, and in particular in combinatorics, the combinatorial number system of degree k, also referred to as combinadics, or the Macaulay representation of an integer, is a correspondence between natural numbers N and k-combinations. The combinations are represented as strictly decreasing sequences c_k > ... > c₂ > c₁ ≥ 0 where each c_i corresponds to the index of a chosen element in a given k-combination. Distinct numbers correspond to distinct k-combinations, and produce them in lexicographic order. The numbers less than $correspond to all k -combinations of {0, 1, ..., n - 1}. The correspondence does not depend on the size n of the set that the k -combinations are taken from, so it can be interpreted as a map from N to the k -combinations taken from N; in this view the correspondence is a bijection.$

In mathematics, the Gaussian binomial coefficients are q-analogs of the binomial coefficients. The Gaussian binomial coefficient, written as $or, is a polynomial in q with integer coefficients, whose value when q is set to a prime power counts the number of subspaces of dimension k in a vector space of dimension n over, a finite field with q elements; i.e. it is the number of points in the finite Grassmannian .$

In mathematics the nth central binomial coefficient is the particular binomial coefficient

In combinatorics, the twelvefold way is a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number. The idea of the classification is credited to Gian-Carlo Rota, and the name was suggested by Joel Spencer.

In number theory, Lucas's theorem expresses the remainder of division of the binomial coefficient $by a prime number p in terms of the base p expansions of the integers m and n .$

In mathematics, Kummer's theorem is a formula for the exponent of the highest power of a prime number p that divides a given binomial coefficient. In other words, it gives the p-adic valuation of a binomial coefficient. The theorem is named after Ernst Kummer, who proved it in a paper,.

References

↑ Batterson, J. Competition Math for Middle School. Art of Problem Solving.
↑ Flajolet, Philippe; Sedgewick, Robert (June 26, 2009). Analytic Combinatorics. Cambridge University Press. ISBN 978-0-521-89806-5.
↑ "Art of Problem Solving". artofproblemsolving.com. Retrieved 2021-10-26.
↑ Feller, William (1968). An Introduction to Probability Theory and Its Applications. Vol. 1 (3rd ed.). Wiley. p. 38.
↑ Ehrenfest, Paul; Kamerlingh Onnes, Heike (1914). "Simplified deduction of the formula from the theory of combinations which Planck uses as the basis of his radiation theory". Proceedings of the KNAW. 17: 870–873. Retrieved 16 May 2024.
↑ Ehrenfest, Paul; Kamerlingh Onnes, Heike (1915). "Simplified deduction of the formula from the theory of combinations which Planck uses as the basis of his radiation theory". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Series 6. 29 (170): 297–301. doi:10.1080/14786440208635308 . Retrieved 5 December 2020.
↑ Planck, Max (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum". Annalen der Physik. 309 (3): 553–563. Bibcode:1901AnP...309..553P. doi: 10.1002/andp.19013090310 .
↑ Gearhart, C. (2002). "Planck, the Quantum, and the Historians" (PDF). Phys. perspect. 4: 170–215. doi:10.1007/s00016-002-8363-7 . Retrieved 16 May 2024.