
An electromagnetic field is a physical field, mathematical functions of position and time, representing the influences on and due to electric charges. The field at any point in space and time can be regarded as a combination of an electric field and a magnetic field. Because of the interrelationship between the fields, a disturbance in the electric field can create a disturbance in the magnetic field which in turn affects the electric field, leading to an oscillation that propagates through space, known as an electromagnetic wave.

In Newtonian mechanics, momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If m is an object's mass and v is its velocity, then the object's momentum p is:
The following outline is provided as an overview of and topical guide to physics:

Quantum mechanics is a fundamental theory in physics that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.

Richard Phillips Feynman was an American theoretical physicist, known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, as well as his work in particle physics for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
Wave–particle duality is the concept in quantum mechanics that quantum entities exhibit particle or wave properties according to the experimental circumstances. It expresses the inability of the classical concepts such as particle or wave to fully describe the behavior of quantum objects. During the 19th and early 20th centuries, light was found to behave as a wave, and then later discovered to have a particulate character, whereas electrons were found to act as particles, and then later discovered to have wavelike aspects. The concept of duality arose to name these contradictions.

Julian Seymour Schwinger was a Nobel Prize-winning American theoretical physicist. He is best known for his work on quantum electrodynamics (QED), in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order. Schwinger was a physics professor at several universities.

A gauge theory is a type of theory in physics. The word gauge means a measurement, a thickness, an in-between distance, or a resulting number of units per certain parameter. Modern theories describe physical forces in terms of fields, e.g., the electromagnetic field, the gravitational field, and fields that describe forces between the elementary particles. A general feature of these field theories is that the fundamental fields cannot be directly measured; however, some associated quantities can be measured, such as charges, energies, and velocities. For example, say you cannot measure the diameter of a lead ball, but you can determine how many lead balls, which are equal in every way, are required to make a pound. Using the number of balls, the density of lead, and the formula for calculating the volume of a sphere from its diameter, one could indirectly determine the diameter of a single lead ball.

In physics, specifically relativistic quantum mechanics (RQM) and its applications to particle physics, relativistic wave equations predict the behavior of particles at high energies and velocities comparable to the speed of light. In the context of quantum field theory (QFT), the equations determine the dynamics of quantum fields. The solutions to the equations, universally denoted as ψ or Ψ, are referred to as "wave functions" in the context of RQM, and "fields" in the context of QFT. The equations themselves are called "wave equations" or "field equations", because they have the mathematical form of a wave equation or are generated from a Lagrangian density and the field-theoretic Euler–Lagrange equations.
In physics, semiclassical refers to a theory in which one part of a system is described quantum mechanically, whereas the other is treated classically. For example, external fields will be constant, or when changing will be classically described. In general, it incorporates a development in powers of Planck's constant, resulting in the classical physics of power 0, and the first nontrivial approximation to the power of (−1). In this case, there is a clear link between the quantum-mechanical system and the associated semi-classical and classical approximations, as it is similar in appearance to the transition from physical optics to geometric optics.
In theoretical physics and applied mathematics, a field equation is a partial differential equation which determines the dynamics of a physical field, specifically the time evolution and spatial distribution of the field. The solutions to the equation are mathematical functions which correspond directly to the field, as functions of time and space. Since the field equation is a partial differential equation, there are families of solutions which represent a variety of physical possibilities. Usually, there is not just a single equation, but a set of coupled equations which must be solved simultaneously. Field equations are not ordinary differential equations since a field depends on space and time, which requires at least two variables.

In particle physics, the history of quantum field theory starts with its creation by Paul Dirac, when he attempted to quantize the electromagnetic field in the late 1920s. Major advances in the theory were made in the 1940s and 1950s, leading to the introduction of renormalized quantum electrodynamics (QED). The field theory behind QED was so accurate and successful in predictions that efforts were made to apply the same basic concepts for the other forces of nature. Beginning in 1954, the parallel was found by way of gauge theory, leading by the late 1970s, to quantum field models of strong nuclear force and weak nuclear force, united in the modern Standard Model of particle physics.
The Wheeler–Feynman absorber theory, named after its originators, the physicists, Richard Feynman, and John Archibald Wheeler, is a theory of electrodynamics based on a relativistic correct extension of action at a distance electron particles. The theory postulates no independent electromagnetic field. Rather, the whole theory is encapsulated by the Lorentz-invariant action of particle trajectories defined as
Asım Orhan Barut was a Turkish-American theoretical physicist.
In physics, relativistic quantum mechanics (RQM) is any Poincaré covariant formulation of quantum mechanics (QM). This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of light c, and can accommodate massless particles. The theory has application in high energy physics, particle physics and accelerator physics, as well as atomic physics, chemistry and condensed matter physics. Non-relativistic quantum mechanics refers to the mathematical formulation of quantum mechanics applied in the context of Galilean relativity, more specifically quantizing the equations of classical mechanics by replacing dynamical variables by operators. Relativistic quantum mechanics (RQM) is quantum mechanics applied with special relativity. Although the earlier formulations, like the Schrödinger picture and Heisenberg picture were originally formulated in a non-relativistic background, a few of them also work with special relativity.

Classical mechanics is a physical theory describing the motion of objects such as projectiles, parts of machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics involved substantial change in the methods and philosophy of physics. The qualifier classical distinguishes this type of mechanics from physics developed after the revolutions in physics of the early 20th century, all of which revealed limitations in classical mechanics.
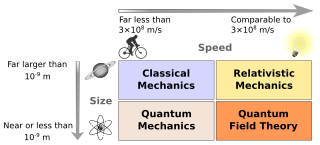
Physics is a scientific discipline that seeks to construct and experimentally test theories of the physical universe. These theories vary in their scope and can be organized into several distinct branches, which are outlined in this article.

The Course of Theoretical Physics is a ten-volume series of books covering theoretical physics that was initiated by Lev Landau and written in collaboration with his student Evgeny Lifshitz starting in the late 1930s.

In physics, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. A weather map, with the surface temperature described by assigning a number to each point on the map, is an example of a scalar field. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.











