

In the mathematical field of graph theory, a toroidal graph is a graph that can be embedded on a torus. In other words, the graph's vertices and edges can be placed on a torus such that no edges intersect except at a vertex that belongs to both.


In the mathematical field of graph theory, a toroidal graph is a graph that can be embedded on a torus. In other words, the graph's vertices and edges can be placed on a torus such that no edges intersect except at a vertex that belongs to both.
Any graph that can be embedded in a plane can also be embedded in a torus, so every planar graph is also a toroidal graph. A toroidal graph that cannot be embedded in a plane is said to have genus 1.
The Heawood graph, the complete graph K7 (and hence K5 and K6), the Petersen graph (and hence the complete bipartite graph K3,3, since the Petersen graph contains a subdivision of it), one of the Blanuša snarks, [1] and all Möbius ladders are toroidal. More generally, any graph with crossing number 1 is toroidal. Some graphs with greater crossing numbers are also toroidal: the Möbius–Kantor graph, for example, has crossing number 4 and is toroidal. [2]
Any toroidal graph has chromatic number at most 7. [3] The complete graph K7 provides an example of a toroidal graph with chromatic number 7. [4]
Any triangle-free toroidal graph has chromatic number at most 4. [5]
By a result analogous to Fáry's theorem, any toroidal graph may be drawn with straight edges in a rectangle with periodic boundary conditions. [6] Furthermore, the analogue of Tutte's spring theorem applies in this case. [7] Toroidal graphs also have book embeddings with at most 7 pages. [8]
By the Robertson–Seymour theorem, there exists a finite set H of minimal non-toroidal graphs, such that a graph is toroidal if and only if it has no graph minor in H. That is, H forms the set of forbidden minors for the toroidal graphs. The complete set H is not known, but it has at least 17,523 graphs. Alternatively, there are at least 250,815 non-toroidal graphs that are minimal in the topological minor ordering. A graph is toroidal if and only if it has none of these graphs as a topological minor. [9]

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain.

Tomaž (Tomo) Pisanski is a Slovenian mathematician working mainly in discrete mathematics and graph theory. He is considered by many Slovenian mathematicians to be the "father of Slovenian discrete mathematics."

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
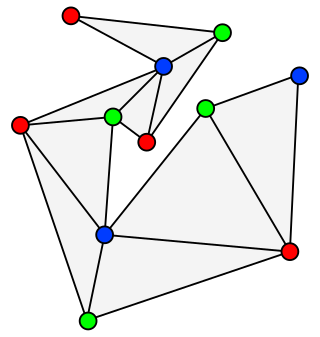
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
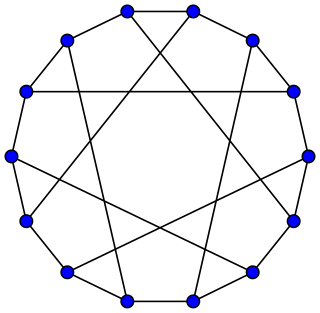
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.

In mathematics, the Heawood number of a surface is an upper bound for the number of colors that suffice to color any graph embedded in the surface.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.
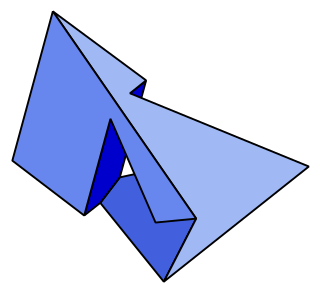
In geometry, the Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

In the mathematical field of graph theory, the Shrikhande graph is a graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having degree 6. Every pair of nodes has exactly two other neighbors in common, whether the pair of nodes is connected or not.
In graph theory, the bipartite double cover of an undirected graph G is a bipartite, covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs, G × K2. It is also called the Kronecker double cover, canonical double cover or simply the bipartite double of G.

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.

In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

In geometry, a toroidal polyhedron is a polyhedron which is also a toroid, having a topological genus of 1 or greater. Notable examples include the Császár and Szilassi polyhedra.

In graph theory, the Golomb graph is a polyhedral graph with 10 vertices and 18 edges. It is named after Solomon W. Golomb, who constructed it as a unit distance graph that requires four colors in any graph coloring. Thus, like the simpler Moser spindle, it provides a lower bound for the Hadwiger–Nelson problem: coloring the points of the Euclidean plane so that each unit line segment has differently-colored endpoints requires at least four colors.