
Enzymes are proteins that act as biological catalysts by accelerating chemical reactions. The molecules upon which enzymes may act are called substrates, and the enzyme converts the substrates into different molecules known as products. Almost all metabolic processes in the cell need enzyme catalysis in order to occur at rates fast enough to sustain life. Metabolic pathways depend upon enzymes to catalyze individual steps. The study of enzymes is called enzymology and the field of pseudoenzyme analysis recognizes that during evolution, some enzymes have lost the ability to carry out biological catalysis, which is often reflected in their amino acid sequences and unusual 'pseudocatalytic' properties.

The reaction rate or rate of reaction is the speed at which a chemical reaction takes place, defined as proportional to the increase in the concentration of a product per unit time and to the decrease in the concentration of a reactant per unit time. Reaction rates can vary dramatically. For example, the oxidative rusting of iron under Earth's atmosphere is a slow reaction that can take many years, but the combustion of cellulose in a fire is a reaction that takes place in fractions of a second. For most reactions, the rate decreases as the reaction proceeds. A reaction's rate can be determined by measuring the changes in concentration over time.

In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions of one substrate and one product. It takes the form of an equation describing the rate reaction rate to , the concentration of the substrate A. Its formula is given by the Michaelis–Menten equation:

Maud Leonora Menten was a Canadian physician and chemist. As a bio-medical and medical researcher, she made significant contributions to enzyme kinetics and histochemistry and invented a procedure that remains in use. She is primarily known for her work with Leonor Michaelis on enzyme kinetics in 1913. The paper has been translated from its original German into English.
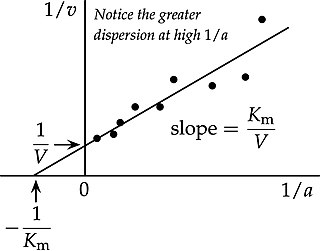
In biochemistry, the Lineweaver–Burk plot is a graphical representation of the Michaelis–Menten equation of enzyme kinetics, described by Hans Lineweaver and Dean Burk in 1934.
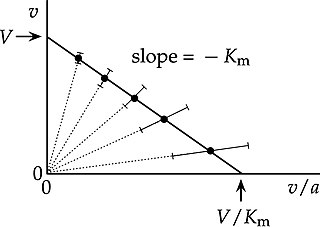
In biochemistry, an Eadie–Hofstee plot is a graphical representation of the Michaelis–Menten equation in enzyme kinetics. It has been known by various different names, including Eadie plot, Hofstee plot and Augustinsson plot. Attribution to Woolf is often omitted, because although Haldane and Stern credited Woolf with the underlying equation, it was just one of the three linear transformations of the Michaelis–Menten equation that they initially introduced. However, Haldane indicated latter that Woolf had indeed found the three linear forms: "In 1932, Dr. Kurt Stern published a German translation of my book "Enzymes", with numerous additions to the English text. On pp. 119-120, I described some graphical methods, stating that they were due to my friend Dr. Barnett Woolf. [...] Woolf pointed out that linear graphs are obtained when is plotted against , against , or against , the first plot being most convenient unless inhibition is being studied."
Non-competitive inhibition is a type of enzyme inhibition where the inhibitor reduces the activity of the enzyme and binds equally well to the enzyme whether or not it has already bound the substrate. This is unlike competitive inhibition, where binding affinity for the substrate in the enzyme is decreased in the presence of an inhibitor.

Enzyme kinetics is the study of the rates of enzyme-catalysed chemical reactions. In enzyme kinetics, the reaction rate is measured and the effects of varying the conditions of the reaction are investigated. Studying an enzyme's kinetics in this way can reveal the catalytic mechanism of this enzyme, its role in metabolism, how its activity is controlled, and how a drug or a modifier might affect the rate.
Uncompetitive inhibition is a type of inhibition in which the apparent values of the Michaelis–Menten parameters and are decreased in the same proportion.

An enzyme inhibitor is a molecule that binds to an enzyme and blocks its activity. Enzymes are proteins that speed up chemical reactions necessary for life, in which substrate molecules are converted into products. An enzyme facilitates a specific chemical reaction by binding the substrate to its active site, a specialized area on the enzyme that accelerates the most difficult step of the reaction.
In the field of biochemistry, the specificity constant, is a measure of how efficiently an enzyme converts substrates into products. A comparison of specificity constants can also be used as a measure of the preference of an enzyme for different substrates. The higher the specificity constant, the more the enzyme "prefers" that substrate.
Myron Lee Bender (1924–1988) was born in St. Louis, Missouri. He obtained his B.S. (1944) and his Ph.D. (1948) from Purdue University. The latter was under the direction of Henry B. Hass. After postdoctoral research under Paul D. Barlett, and Frank H. Westheimer, he spent one year as a faculty member at the University of Connecticut. Thereafter, he was a professor of Chemistry at Illinois Institute of Technology in 1951, and then at Northwestern University in 1960. He worked primarily in the study of reaction mechanisms and the biochemistry of enzyme action. Myron L. Bender demonstrated the two-step mechanism of catalysis for serine proteases, nucleophilic catalysis in ester hydrolysis and intramolecular catalysis in water. He also showed that cyclodextrin can be used to investigate catalysis of organic reactions within the scope of host–guest chemistry. Finally, he and others reported on the synthesis of an organic compound as a model of an acylchymotrypsin intermediate.

In biochemistry, a Hanes–Woolf plot, Hanes plot, or plot of against , is a graphical representation of enzyme kinetics in which the ratio of the initial substrate concentration to the reaction velocity is plotted against . It is based on the rearrangement of the Michaelis–Menten equation shown below:

Victor Henri was a French-Russian physical chemist and physiologist. He was born in Marseilles as a son of Russian parents. He is known mainly as an early pioneer in enzyme kinetics. He published more than 500 papers in a variety of disciplines including biochemistry, physical chemistry, psychology, and physiology. Aleksey Krylov was his half-brother.

A diffusion-limited enzyme catalyses a reaction so efficiently that the rate limiting step is that of substrate diffusion into the active site, or product diffusion out. This is also known as kinetic perfection or catalytic perfection. Since the rate of catalysis of such enzymes is set by the diffusion-controlled reaction, it therefore represents an intrinsic, physical constraint on evolution. Diffusion limited perfect enzymes are very rare. Most enzymes catalyse their reactions to a rate that is 1,000-10,000 times slower than this limit. This is due to both the chemical limitations of difficult reactions, and the evolutionary limitations that such high reaction rates do not confer any extra fitness.

In enzyme kinetics, a secondary plot uses the intercept or slope from several Lineweaver–Burk plots to find additional kinetic constants.
The dissociation rate in chemistry, biochemistry, and pharmacology is the rate or speed at which a ligand dissociates from a protein, for instance, a receptor. It is an important factor in the binding affinity and intrinsic activity (efficacy) of a ligand at a receptor. The dissociation rate for a particular substrate can be applied to enzyme kinetics, including the Michaelis-Menten model. Substrate dissociation rate contributes to how large or small the enzyme velocity will be. In the Michaelis-Menten model, the enzyme binds to the substrate yielding an enzyme substrate complex, which can either go backwards by dissociating or go forward by forming a product. The dissociation rate constant is defined using Koff.
In electrochemistry, protein film voltammetry is a technique for examining the behavior of proteins immobilized on an electrode. The technique is applicable to proteins and enzymes that engage in electron transfer reactions and it is part of the methods available to study enzyme kinetics.
Competitive inhibition is interruption of a chemical pathway owing to one chemical substance inhibiting the effect of another by competing with it for binding or bonding. Any metabolic or chemical messenger system can potentially be affected by this principle, but several classes of competitive inhibition are especially important in biochemistry and medicine, including the competitive form of enzyme inhibition, the competitive form of receptor antagonism, the competitive form of antimetabolite activity, and the competitive form of poisoning.
In chemistry, catalytic resonance theory was developed to describe the kinetics of reaction acceleration using dynamic catalyst surfaces. Catalytic reactions occurring on surfaces that undergo variation in surface binding energy and/or entropy exhibit overall increase in reaction rate when the surface binding energy frequencies are comparable to the natural frequencies of the surface reaction, adsorption, and desorption.


















