Related Research Articles

Crystallography is the experimental science of determining the arrangement of atoms in crystalline solids. Crystallography is a fundamental subject in the fields of materials science and solid-state physics. The word crystallography is derived from the Ancient Greek word κρύσταλλος, and γράφειν. In July 2012, the United Nations recognised the importance of the science of crystallography by proclaiming that 2014 the International Year of Crystallography.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

In geometry, a glide reflection or transflection is a geometric transformation that consists of a reflection across a hyperplane and a translation ("glide") in a direction parallel to that hyperplane, combined into a single transformation. Because the distances between points are not changed under glide reflection, it is a motion or isometry. When the context is the two-dimensional Euclidean plane, the hyperplane of reflection is a straight line called the glide line or glide axis. When the context is three-dimensional space, the hyperplane of reflection is a plane called the glide plane. The displacement vector of the translation is called the glide vector.

In crystallography, a crystal system is a set of point groups. A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family.
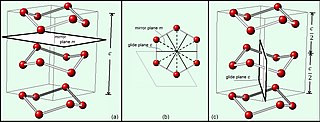
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.

In geometry and crystallography, a Bravais lattice, named after Auguste Bravais, is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
In crystallography, a crystallographic point group is a three dimensional point group whose symmetry operations are compatible with a three dimensional crystallographic lattice. According to the crystallographic restriction it may only contain one-, two-, three-, four- and sixfold rotations or rotoinversions. This reduces the number of crystallographic point groups to 32. These 32 groups are one-and-the-same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms.

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.

In geometry, a point group is a mathematical group of symmetry operations (isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension d is then a subgroup of the orthogonal group O(d). Point groups are used to describe the symmetries of geometric figures and physical objects such as molecules.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.

In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.
In chemistry and crystallography, a symmetry element is a point, line, or plane about which symmetry operations can take place. In particular, a symmetry element can be a mirror plane, an axis of rotation, or a center of inversion. For an object such as a molecule or a crystal, a symmetry element corresponds to a set of symmetry operations, which are the rigid transformations employing the symmetry element that leave the object unchanged. The set containing these operations form one of the symmetry groups of the object. The elements of this symmetry group should not be confused with the "symmetry element" itself. Loosely, a symmetry element is the geometric set of fixed points of a symmetry operation. For example, for rotation about an axis, the points on the axis do not move and in a reflection the points that remain unchanged make up a plane of symmetry.
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a 1⁄3 turn rotation of a regular triangle about its center, a reflection of a square across its diagonal, a translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element. Symmetry operations can be classified either as point symmetry operations or as travel symmetry operations.

In geometry, a point reflection is a transformation of affine space in which every point is reflected across a specific fixed point. When dealing with crystal structures and in the physical sciences the terms inversion symmetry, inversion center or centrosymmetric are more commonly used.

In crystallography, the hexagonal crystal family is one of the 6 crystal families, which includes two crystal systems and two lattice systems. While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent. In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice.
In geometry, a polar point group is a point group in which there is more than one point that every symmetry operation leaves unmoved. The unmoved points will constitute a line, a plane, or all of space.
References
- ↑ Lev. Kantorovich (2004). Quantum Theory of the Solid State: An Introduction. Springer. p. 28.
- ↑ "Not so elementary, my dear Wyckoff". www.iucr.org. Retrieved 2023-01-06.
- ↑ Wyckoff, Ralph W. G. (1922). The analytical expression of the results of the theory of space-groups. Carnegie Institute of Washington. OCLC 3557642.
- ↑ Halford, Ralph S. (1946). "Motions of Molecules in Condensed Systems: I. Selection Rules, Relative Intensities, and Orientation Effects for Raman and Infra‐Red Spectra". The Journal of Chemical Physics. 14 (1). AIP Publishing: 8–15. doi:10.1063/1.1724065. ISSN 0021-9606.
- ↑ Donald Sands (1975). "Crystal Systems and Geometry". Introduction to Crystallography (PDF). pp. 75–76. ISBN 0-486-67839-3.
- ↑ International tables for crystallography. Chester, England: International Union of Crystallography. 2006. doi:10.1107/97809553602060000001. ISBN 978-0-7923-6590-7. OCLC 166325528.