A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's seed. Although sequences that are closer to truly random can be generated using hardware random number generators, pseudorandom number generators are important in practice for their speed in number generation and their reproducibility.

A linear congruential generator (LCG) is an algorithm that yields a sequence of pseudo-randomized numbers calculated with a discontinuous piecewise linear equation. The method represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is relatively easy to understand, and they are easily implemented and fast, especially on computer hardware which can provide modular arithmetic by storage-bit truncation.
The Mersenne Twister is a general-purpose pseudorandom number generator (PRNG) developed in 1997 by Makoto Matsumoto and Takuji Nishimura. Its name derives from the choice of a Mersenne prime as its period length.
A Lagged Fibonacci generator is an example of a pseudorandom number generator. This class of random number generator is aimed at being an improvement on the 'standard' linear congruential generator. These are based on a generalisation of the Fibonacci sequence.
In computing, a linear-feedback shift register (LFSR) is a shift register whose input bit is a linear function of its previous state.
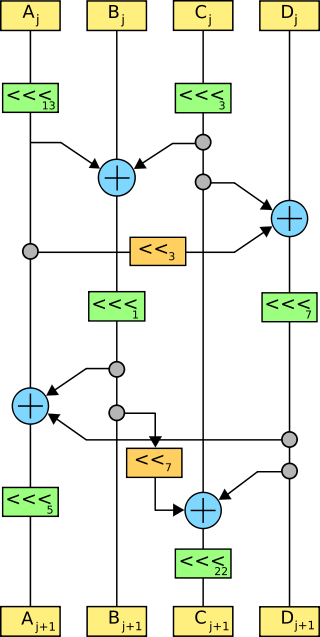
Serpent is a symmetric key block cipher that was a finalist in the Advanced Encryption Standard (AES) contest, in which it ranked second to Rijndael. Serpent was designed by Ross Anderson, Eli Biham, and Lars Knudsen.
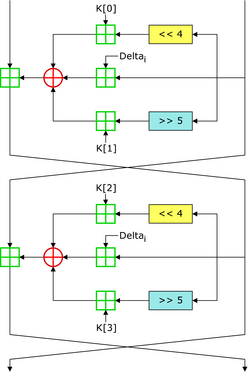
In cryptography, the Tiny Encryption Algorithm (TEA) is a block cipher notable for its simplicity of description and implementation, typically a few lines of code. It was designed by David Wheeler and Roger Needham of the Cambridge Computer Laboratory; it was first presented at the Fast Software Encryption workshop in Leuven in 1994, and first published in the proceedings of that workshop.

In cryptography, XTEA is a block cipher designed to correct weaknesses in TEA. The cipher's designers were David Wheeler and Roger Needham of the Cambridge Computer Laboratory, and the algorithm was presented in an unpublished technical report in 1997. It is not subject to any patents.
Red Pike is a classified United Kingdom government encryption algorithm, proposed for use by the National Health Service by GCHQ, but designed for a "broad range of applications in the British government" Archived 2004-04-23 at the Wayback Machine. Little is publicly known about Red Pike, except that it is a block cipher with a 64-bit block size and 64-bit key length. According to the academic study of the cipher cited below and quoted in a paper by Ross Anderson and Markus Kuhn, it "uses the same basic operations as RC5" and "has no look-up tables, virtually no key schedule and requires only five lines of code"; "the influence of each key bit quickly cascades" and "each encryption involves of the order of 100 operations". 64 bits of key entropy are not considered secure anymore.
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string, or the digit sum of the binary representation of a given number and the ℓ₁ norm of a bit vector. In this binary case, it is also called the population count, popcount, sideways sum, or bit summation.
The grid method of multiplication is an introductory approach to multi-digit multiplication calculations that involve numbers larger than ten. Because it is often taught in mathematics education at the level of primary school or elementary school, this algorithm is sometimes called the grammar school method.
In computer science, multiply-with-carry (MWC) is a method invented by George Marsaglia for generating sequences of random integers based on an initial set from two to many thousands of randomly chosen seed values. The main advantages of the MWC method are that it invokes simple computer integer arithmetic and leads to very fast generation of sequences of random numbers with immense periods, ranging from around to .
The Lehmer random number generator, sometimes also referred to as the Park–Miller random number generator, is a type of linear congruential generator (LCG) that operates in multiplicative group of integers modulo n. The general formula is
In the C programming language, operations can be performed on a bit level using bitwise operators.
TestU01 is a software library, implemented in the ANSI C language, that offers a collection of utilities for the empirical randomness testing of random number generators (RNGs). The library was first introduced in 2007 by Pierre L’Ecuyer and Richard Simard of the Université de Montréal.

The spectral test is a statistical test for the quality of a class of pseudorandom number generators (PRNGs), the linear congruential generators (LCGs). LCGs have a property that when plotted in 2 or more dimensions, lines or hyperplanes will form, on which all possible outputs can be found. The spectral test compares the distance between these planes; the further apart they are, the worse the generator is. As this test is devised to study the lattice structures of LCGs, it can not be applied to other families of PRNGs.
KISS (Keep it Simple Stupid) is a family of pseudorandom number generators introduced by George Marsaglia. Starting from 1998 Marsaglia posted on various newsgroups including sci.math, comp.lang.c, comp.lang.fortran and sci.stat.math several versions of the generators. All KISS generators combine three or four independent random number generators with a view to improving the quality of randomness. KISS generators produce 32-bit or 64-bit random integers, from which random floating-point numbers can be constructed if desired. The original 1993 generator is based on the combination of a linear congruential generator and of two linear feedback shift-register generators. It has a period 295, good speed and good statistical properties; however, it fails the LinearComplexity test in the Crush and BigCrush tests of the TestU01 suite. A newer version from 1999 is based on a linear congruential generator, a 3-shift linear feedback shift-register and two multiply-with-carry generators. It is 10–20% slower than the 1993 version but has a larger period 2123 and passes all tests in TestU01. In 2009 Marsaglia presented a version based on 64-bit integers (appropriate for 64-bit processors) which combines a multiply-with-carry generator, a Xorshift generator and a linear congruential generator. It has a period of around 2250 (around 1075).
xoroshiro128+ is a pseudorandom number generator intended as a successor to xorshift+. Instead of perpetuating Marsaglia's tradition of xorshift as a basic operation, xoroshiro128+ uses a shift/rotate-based linear transformation designed by Sebastiano Vigna in collaboration with David Blackman. The result is a significant improvement in speed and statistical quality.
A permuted congruential generator (PCG) is a pseudorandom number generation algorithm developed in 2014 by Dr. M.E. O'Neill which applies an output permutation function to improve the statistical properties of a modulo-2n linear congruential generator. It achieves excellent statistical performance with small and fast code, and small state size.





