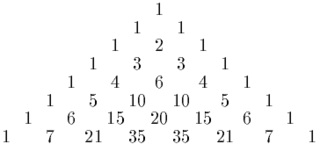
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy.
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is chairman of the OEIS Foundation.

In mathematics, Pascal's pyramid is a three-dimensional arrangement of the trinomial numbers, which are the coefficients of the trinomial expansion and the trinomial distribution. Pascal's pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial numbers and relates to the binomial expansion and the binomial distribution. The binomial and trinomial numbers, coefficients, expansions, and distributions are subsets of the multinomial constructs with the same names.

A pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left.

The lazy caterer's sequence, more formally known as the central polygonal numbers, describes the maximum number of pieces of a disk that can be made with a given number of straight cuts. For example, three cuts across a pancake will produce six pieces if the cuts all meet at a common point inside the circle, but up to seven if they do not. This problem can be formalized mathematically as one of counting the cells in an arrangement of lines; for generalizations to higher dimensions, see arrangement of hyperplanes.
In mathematics the nth central binomial coefficient is the particular binomial coefficient
In mathematics, the boustrophedon transform is a procedure which maps one sequence to another. The transformed sequence is computed by an "addition" operation, implemented as if filling a triangular array in a boustrophedon manner—as opposed to a "Raster Scan" sawtooth-like manner.

In mathematics, the cake number, denoted by Cn, is the maximum number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake.
Lozanić's triangle is a triangular array of binomial coefficients in a manner very similar to that of Pascal's triangle. It is named after the Serbian chemist Sima Lozanić, who researched it in his investigation into the symmetries exhibited by rows of paraffins.
Singmaster's conjecture is a conjecture in combinatorial number theory in mathematics, named after the British mathematician David Singmaster who proposed it in 1971. It says that there is a finite upper bound on the multiplicities of entries in Pascal's triangle. It is clear that the only number that appears infinitely many times in Pascal's triangle is 1, because any other number x can appear only within the first x + 1 rows of the triangle.
In mathematics, a fractal sequence is one that contains itself as a proper subsequence. An example is
The Leibniz harmonic triangle is a triangular arrangement of unit fractions in which the outermost diagonals consist of the reciprocals of the row numbers and each inner cell is the cell diagonally above and to the left minus the cell to the left. To put it algebraically, L(r, 1) = 1/r and L(r, c) = L(r − 1, c − 1) − L(r, c − 1).
In combinatorics, the Narayana numbers form a triangular array of natural numbers, called the Narayana triangle, that occur in various counting problems. They are named after Canadian mathematician T. V. Narayana (1930–1987).
In mathematics, a Delannoy number describes the number of paths from the southwest corner of a rectangular grid to the northeast corner, using only single steps north, northeast, or east. The Delannoy numbers are named after French army officer and amateur mathematician Henri Delannoy.
In mathematics, the Schröder number also called a large Schröder number or big Schröder number, describes the number of lattice paths from the southwest corner of an grid to the northeast corner using only single steps north, northeast, or east, that do not rise above the SW–NE diagonal.

In mathematics, the Bell triangle is a triangle of numbers analogous to Pascal's triangle, whose values count partitions of a set in which a given element is the largest singleton. It is named for its close connection to the Bell numbers, which may be found on both sides of the triangle, and which are in turn named after Eric Temple Bell. The Bell triangle has been discovered independently by multiple authors, beginning with Charles Sanders Peirce (1880) and including also Alexander Aitken (1933) and Cohn et al. (1962), and for that reason has also been called Aitken's array or the Peirce triangle.
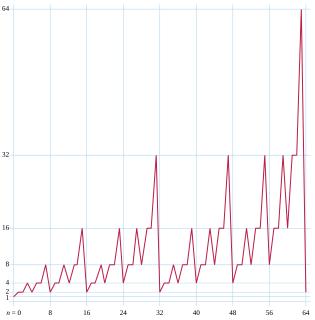
Gould's sequence is an integer sequence named after Henry W. Gould that counts the odd numbers in each row of Pascal's triangle. It consists only of powers of two, and begins:

Bernoulli's triangle is an array of partial sums of the binomial coefficients. For any non-negative integer n and for any integer k included between 0 and n, the component in row n and column k is given by:

In combinatorics, tripod packing is a problem of finding many disjoint tripods in a three-dimensional grid, where a tripod is an infinite polycube, the union of the grid cubes along three positive axis-aligned rays with a shared apex.
In the number theory of integer partitions, the numbers denote both the number of partitions of into exactly parts, and the number of partitions of into parts of maximum size exactly . These two types of partition are in bijection with each other, by a diagonal reflection of their Young diagrams. Their numbers can be arranged into a triangle, the triangle of partition numbers, in which the th row gives the partition numbers :











