In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own boolean-valued outcome: a random variable containing a single bit of information: success/yes/true/one or failure/no/false/zero. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.
Generally speaking, a calendar year begins on the New Year's Day of the given calendar system and ends on the day before the following New Year's Day, and thus consists of a whole number of days. A year can also be measured by starting on any other named day of the calendar, and ending on the day before this named day in the following year. This may be termed a "year's time", but not a "calendar year". To reconcile the calendar year with the astronomical cycle certain years contain extra days.
In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.
In statistics, the standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of data values. A low standard deviation indicates that the data points tend to be close to the mean of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values.
In probability theory and statistics, the geometric distribution is either of two discrete probability distributions:
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written as
![Dead Sea Scrolls Ancient Jewish religious, mostly Hebrew, manuscripts found in the Qumran Caves in the West Bank] near the Dead Sea](https://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/Flag_of_Israel.svg/320px-Flag_of_Israel.svg.png)
The Dead Sea Scrolls are ancient Jewish religious, mostly Hebrew, manuscripts found in the Qumran Caves in the West Bank near the Dead Sea. Scholarly consensus dates these scrolls from the last three centuries BCE and the first century CE. The texts have great historical, religious, and linguistic significance because they include the second-oldest known surviving manuscripts of works later included in the Hebrew Bible canon, along with deuterocanonical and extra-biblical manuscripts which preserve evidence of the diversity of religious thought in late Second Temple Judaism. Almost all of the Dead Sea Scrolls collection is currently under the ownership of the Government of the state of Israel, and housed in the Shrine of the Book on the grounds of the Israel Museum.
In mathematics, factorization or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is a factorization of the integer 15, and (x – 2)(x + 2) is a factorization of the polynomial x2 – 4.
In abstract algebra and formal logic, the distributive property of binary operations generalizes the distributive law from Boolean algebra and elementary algebra. In propositional logic, distribution refers to two valid rules of replacement. The rules allow one to reformulate conjunctions and disjunctions within logical proofs.
Capacitance is the ratio of the change in an electric charge in a system to the corresponding change in its electric potential. There are two closely related notions of capacitance: self capacitance and mutual capacitance. Any object that can be electrically charged exhibits self capacitance. A material with a large self capacitance holds more electric charge at a given voltage than one with low capacitance. The notion of mutual capacitance is particularly important for understanding the operations of the capacitor, one of the three elementary linear electronic components.
In algebra, the partial fraction decomposition or partial fraction expansion of a rational function is an operation that consists of expressing the fraction as a sum of a polynomial and one or several fractions with a simpler denominator.
In mathematics, E6 is the name of some closely related Lie groups, linear algebraic groups or their Lie algebras , all of which have dimension 78; the same notation E6 is used for the corresponding root lattice, which has rank 6. The designation E6 comes from the Cartan–Killing classification of the complex simple Lie algebras (see Élie Cartan § Work). This classifies Lie algebras into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8, F4, and G2. The E6 algebra is thus one of the five exceptional cases.
The DHC-8 Dash 8 is a series of turboprop-powered regional airliners, introduced by de Havilland Canada (DHC) in 1984. DHC was later bought by Boeing in 1988, then by Bombardier in 1992; the program is to be resold to Viking Air parent Longview Aviation Capital by late 2019. Powered by two Pratt & Whitney Canada PW100s, it was developed from the Dash 7 with improved cruise performance, lowered operational costs but worse STOL performance. Three sizes were offered: initially the 37-40 seat -100 until 2005 and the more powerful -200 from 1995, the stretched 50-56 seats -300 from 1989, both until 2009, and the 68-90 seats -400 from 1999, still in production. The Q Series are post-1997 variants with quieter cabins.
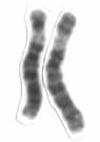
Chromosome 6 is one of the 23 pairs of chromosomes in humans. People normally have two copies of this chromosome. Chromosome 6 spans more than 170 million base pairs and represents between 5.5 and 6% of the total DNA in cells. It contains the Major Histocompatibility Complex, which contains over 100 genes related to the immune response, and plays a vital role in organ transplantation.
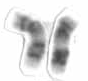
Chromosome 17 is one of the 23 pairs of chromosomes in humans. People normally have two copies of this chromosome. Chromosome 17 spans more than 83 million base pairs and represents between 2.5 and 3% of the total DNA in cells.
ICD-10 is an international statistical classification used in health care and related industries.
DiGeorge syndrome, also known as 22q11.2 deletion syndrome, is a syndrome caused by the deletion of a small segment of chromosome 22. While the symptoms can be variable, they often include congenital heart problems, specific facial features, frequent infections, developmental delay, learning problems and cleft palate. Associated conditions include kidney problems, hearing loss and autoimmune disorders such as rheumatoid arthritis or Graves disease.
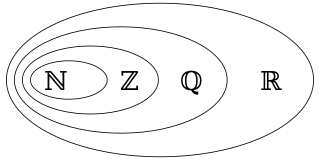
In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q ; it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
Coulomb's law, or Coulomb's inverse-square law, is a law of physics for quantifying Coulomb's force, or electrostatic force. Electrostatic force is the amount of force with which stationary, electrically charged particles either repel, or attract each other. This force and the law for quantifying it, represent one of the most basic forms of force used in the physical sciences, and were an essential basis to the study and development of the theory and field of classical electromagnetism. The law was first published in 1785 by French physicist Charles-Augustin de Coulomb.
