Acceptance angle (solar concentrator)

Last updated February 05, 2024

Acceptance angle is the maximum angle at which incoming sunlight can be captured by a solar concentrator. Its value depends on the concentration of the optic and the refractive index in which the receiver is immersed. Maximizing the acceptance angle of a concentrator is desirable in practical systems and it may be achieved by using nonimaging optics.

Definition

The "acceptance angle" figure illustrates this concept.

The concentrator is a lens with a receiver R. The left section of the figure shows a set of parallel rays incident on the concentrator at an angle α < θ to the optical axis. All rays end up on the receiver and, therefore, all light is captured. In the center, this figure shows another set of parallel rays, now incident on the concentrator at an angle α = θ to the optical axis. For an ideal concentrator, all rays are still captured. However, on the right, this figure shows yet another set of parallel rays, now incident on the concentrator at an angle α > θ to the optical axis. All rays now miss the receiver and all light is lost. Therefore, for incidence angles α < θ all light is captured while for incidence angles α > θ all light is lost. The concentrator is then said to have a (half) acceptance angle θ, or a total acceptance angle 2θ (since it accepts light within an angle ±θ to the optical axis).

Ideally, a solar concentrator has a transmission curve c_I as shown in the "transmission curves" figure. Transmission (efficiency) is τ = 1 for all incidence angles α < θ_I and τ = 0 for all incidence angles α > θ_I.

In practice, real transmission curves are not perfect and they typically have a shape similar to that of curve c_R, which is normalized so that τ = 1 for α = 0. In that case, the real acceptance angle θ_R is typically defined as the angle for which transmission τ drops to 90% of its maximum.^[1]

For line-focus systems, such as a trough concentrator or a linear Fresnel lens, the acceptance angle is one dimensional, and the concentration has only weak dependence on off-pointing perpendicular to the focus direction. Point focus systems, on the other hand, are sensitive to off-pointing in both directions. In the general case, the acceptance angle in one direction may be different from the other.

Acceptance angle as a tolerance budget

The acceptance angle θ of a concentrator may be seen as a measure of how precisely it must track the sun in the sky. The smaller the θ, the more precise the tracking needs to be or the concentrator will not capture the incoming sunlight. It is, therefore, a measure of the tolerance a concentrator has to tracking errors.

However, other errors also affect the acceptance angle. The "optical imperfections" figure shows this.

The left part of the figure shows a perfectly made lens with good optical surfaces s₁ and s₂ capturing all light rays incident at an angle α to the optical axis. However, real optics are never perfect and the right part of the figure shows the effect of a badly made bottom surface s₂. Instead of being smooth, s₂ now has undulations and some of the light rays that were captured before are now lost. This decreases the transmission of the concentrator for incidence angle α, decreasing the acceptance angle. Actually, any imperfection in the system such as:

tracking inaccuracy
imperfectly manufactured optics
optical aberrations
imperfectly assembled components
movements of the system due to wind
finite stiffness of the supporting structure
deformation due to aging
other imperfections in the system

contributes to a decrease in the acceptance angle of the concentrator. The acceptance angle may then be seen as a "tolerance budget" to be spent on all these imperfections. At the end, the concentrator must still have enough acceptance to capture sunlight which also has some angular dispersion θ_S when seen from earth. It is, therefore, very important to design a concentrator with the widest possible acceptance angle. That is possible using nonimaging optics, which maximize the acceptance angle for a given concentration.

Figure "angular aperture of sunlight" on the right shows the effect of the angular dispersion of sunlight on the acceptance angle.

Sunlight is not a set of perfectly parallel rays (shown in blue), but it has a given angular aperture θ_S, as indicated by the green rays. If the acceptance angle of the optic is wide enough, sunlight incident along the optical axis will be captured by the concentrator, as shown in the "angular aperture of sunlight" figure. However, for wider incidence angles α some light may be lost, as shown on the right. Perfectly parallel rays (shown in blue) would be captured, but sunlight, due to its angular aperture, is partially lost.

Parallel rays and sunlight are therefore transmitted differently by a solar concentrator and the corresponding transmission curves are also different. Different acceptance angles may then be determined for parallel rays or for sunlight.

Concentration acceptance product (CAP)

For a given acceptance angle θ, for a point-focus concentrator, the maximum concentration possible, C_max, is given by

C_{\mathrm {max} }={\frac {n^{2}}{\sin ^{2}\theta }}

,

where n is the refractive index of the medium in which the receiver is immersed.^[2] In practice, real concentrators either have a lower than ideal concentration for a given acceptance or they have a lower than ideal acceptance angle for a given concentration. This can be summarized in the expression

CAP={\sqrt {C}}\sin \theta \leq n

,

which defines a quantity CAP (concentration acceptance product), which must be smaller than the refractive index of the medium in which the receiver is immersed.

For a linear-focused concentrator, the equation is not squared^[3]

C_{\mathrm {max} }={\frac {n}{\sin \theta }}

The Concentration Acceptance Product is a consequence of the conservation of etendue. The higher the CAP, the closer the concentrator is to the maximum possible in concentration and acceptance angle.

Related Research Articles

$Diffraction Phenomenon of the motion of waves$

Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1660.

The Fresnel equations describe the reflection and transmission of light when incident on an interface between different optical media. They were deduced by French engineer and physicist Augustin-Jean Fresnel who was the first to understand that light is a transverse wave, when no one realized that the waves were electric and magnetic fields. For the first time, polarization could be understood quantitatively, as Fresnel's equations correctly predicted the differing behaviour of waves of the s and p polarizations incident upon a material interface.

In optics, polarized light can be described using the Jones calculus, invented by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by Jones matrices. When light crosses an optical element the resulting polarization of the emerging light is found by taking the product of the Jones matrix of the optical element and the Jones vector of the incident light. Note that Jones calculus is only applicable to light that is already fully polarized. Light which is randomly polarized, partially polarized, or incoherent must be treated using Mueller calculus.

<span class="mw-page-title-main">Optics</span> Branch of physics that studies light

Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Light is a type of electromagnetic radiation, and other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.

A guided ray is a ray of light in a multi-mode optical fiber, which is confined by the core.

In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another, provided there is no refractive power at the interface. The exact definition of the term varies slightly between different areas of optics. Numerical aperture is commonly used in microscopy to describe the acceptance cone of an objective, and in fiber optics, in which it describes the range of angles within which light that is incident on the fiber will be transmitted along it.

$Snell's law Formula for refraction angles$

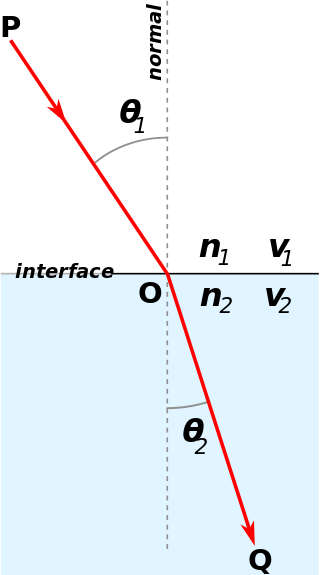
Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index.

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.

Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.

$Airy disk Diffraction pattern in optics$

In optics, the Airy disk and Airy pattern are descriptions of the best-focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light. The Airy disk is of importance in physics, optics, and astronomy.

In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.

In optics, the Abbe sine condition is a condition that must be fulfilled by a lens or other optical system in order for it to produce sharp images of off-axis as well as on-axis objects. It was formulated by Ernst Abbe in the context of microscopes.

Etendue or étendue is a property of light in an optical system, which characterizes how "spread out" the light is in area and angle. It corresponds to the beam parameter product (BPP) in Gaussian beam optics. Other names for etendue include acceptance, throughput, light grasp, light-gathering power, optical extent, and the AΩ product. Throughput and AΩ product are especially used in radiometry and radiative transfer where it is related to the view factor. It is a central concept in nonimaging optics.

Nonimaging optics is the branch of optics concerned with the optimal transfer of light radiation between a source and a target. Unlike traditional imaging optics, the techniques involved do not attempt to form an image of the source; instead an optimized optical system for optimal radiative transfer from a source to a target is desired.

Angular distance or angular separation is the measure of the angle between the orientation of two straight lines, rays, or vectors in three-dimensional space, or the central angle subtended by the radii through two points on a sphere. When the rays are lines of sight from an observer to two points in space, it is known as the apparent distance or apparent separation.

In Gaussian optics, the cardinal points consist of three pairs of points located on the optical axis of a rotationally symmetric, focal, optical system. These are the focal points, the principal points, and the nodal points; there are two of each. For ideal systems, the basic imaging properties such as image size, location, and orientation are completely determined by the locations of the cardinal points; in fact, only four points are necessary: the two focal points and either the principal points or the nodal points. The only ideal system that has been achieved in practice is a plane mirror, however the cardinal points are widely used to approximate the behavior of real optical systems. Cardinal points provide a way to analytically simplify an optical system with many components, allowing the imaging characteristics of the system to be approximately determined with simple calculations.

In optics, a dispersive prism is an optical prism that is used to disperse light, that is, to separate light into its spectral components. Different wavelengths (colors) of light will be deflected by the prism at different angles. This is a result of the prism material's index of refraction varying with wavelength (dispersion). Generally, longer wavelengths (red) undergo a smaller deviation than shorter wavelengths (blue). The dispersion of white light into colors by a prism led Sir Isaac Newton to conclude that white light consisted of a mixture of different colors.

<span class="mw-page-title-main">Acousto-optics</span> The study of sound and light interaction

Acousto-optics is a branch of physics that studies the interactions between sound waves and light waves, especially the diffraction of laser light by ultrasound through an ultrasonic grating.

<span class="mw-page-title-main">22° halo</span> Atmospheric optical phenomenon

A 22° halo is an atmospheric optical phenomenon that consists of a halo with an apparent radius of approximately 22° around the Sun or Moon. When visible around the Moon, it is also known as a moon ring, storm ring, or winter halo. It forms as sunlight or moonlight is refracted by millions of hexagonal ice crystals suspended in the atmosphere. Its radius, as viewed from Earth, is roughly the length of an outstretched hand at arm's length.

The contrast transfer function (CTF) mathematically describes how aberrations in a transmission electron microscope (TEM) modify the image of a sample. This contrast transfer function (CTF) sets the resolution of high-resolution transmission electron microscopy (HRTEM), also known as phase contrast TEM.

References

↑ Benitez, Pablo; et al. (26 April 2010). "High performance Fresnel-based photovoltaic concentrator". Optics Express. 18 (S1): A25-40. Bibcode:2010OExpr..18S..25B. doi: 10.1364/OE.18.000A25 . PMID 20588570.
↑ Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. ISBN 978-1482206739.
↑ See: http://www.powerfromthesun.net/Book/chapter09/chapter09.html . Note that in this derivation theta is the full angle, not the half-angle defined here.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FK-1] Benitez, Pablo; et al. (26 April 2010). "High performance Fresnel-based photovoltaic concentrator". Optics Express. 18 (S1): A25-40. Bibcode:2010OExpr..18S..25B. doi: 10.1364/OE.18.000A25 . PMID 20588570.

[IntroNio2e-2] Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. ISBN 978-1482206739.

[3] See: http://www.powerfromthesun.net/Book/chapter09/chapter09.html . Note that in this derivation theta is the full angle, not the half-angle defined here.

[1]

[2]

[3]