Addition principle

Last updated May 07, 2024

5+0=5 illustrated with collections of dots. AdditionZero.svg — 5+0=5 illustrated with collections of dots.

In combinatorics, the addition principle^[1]^[2] or rule of sum^[3]^[4] is a basic counting principle. Stated simply, it is the intuitive idea that if we have A number of ways of doing something and B number of ways of doing another thing and we can not do both at the same time, then there are $A+B$ ways to choose one of the actions.^[3]^[1] In mathematical terms, the addition principle states that, for disjoint sets A and B, we have $|A\cup B|=|A|+|B|$ ,^[2] provided that the intersection of the sets is without any elements.

Simple example

3+2=5 illustrated with shapes. AdditionShapes.svg — 3+2=5 illustrated with shapes.

A person has decided to shop at one store today, either in the north part of town or the south part of town. If they visit the north part of town, they will shop at either a mall, a furniture store, or a jewelry store (3 ways). If they visit the south part of town then they will shop at either a clothing store or a shoe store (2 ways).

Thus there are $3+2=5$ possible shops the person could end up shopping at today.

Inclusion–exclusion principle

A series of Venn diagrams illustrating the principle of inclusion-exclusion. Inclusion-exclusion-3sets.png — A series of Venn diagrams illustrating the principle of inclusion-exclusion.

The inclusion–exclusion principle (also known as the sieve principle^[7]) can be thought of as a generalization of the rule of sum in that it too enumerates the number of elements in the union of some sets (but does not require the sets to be disjoint). It states that if A₁, ..., A_n are finite sets, then^[7]

\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{i=1}^{n}\left|A_{i}\right|-\sum _{i,j\,:\,1\leq i<j\leq n}\left|A_{i}\cap A_{j}\right|+\sum _{i,j,k\,:\,1\leq i<j<k\leq n}\left|A_{i}\cap A_{j}\cap A_{k}\right|-\ \cdots \ +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.

Subtraction principle

Similarly, for a given finite set S, and given another set A, if $A\subset S$ , then $|A^{c}|=|S|-|A|$ .^[8]^[9] To prove this, notice that $|A^{c}|+|A|=|S|$ by the addition principle.^[9]

Applications

The addition principle can be used to prove Pascal's rule combinatorially. To calculate ${\binom {n+1}{k}}$ , one can view it as the number of ways to choose k people from a room containing n children and 1 teacher. Then there are ${\binom {n}{k}}$ ways to choose people without choosing the teacher, and ${\binom {n}{k-1}}$ ways to choose people that includes the teacher. Thus ${\binom {n+1}{k}}={\binom {n}{k}}+{\binom {n}{k-1}}$ .^[10]^: 83

The addition principle can also be used to prove the multiplication principle.^[2]

Related Research Articles

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n; this coefficient can be computed by the multiplicative formula$

In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial $(x + y) n$ into a sum involving terms of the form $ax b y c$ , where the exponents $b$ and $c$ are nonnegative integers with $b + c = n$ , and the coefficient $a$ of each term is a specific positive integer depending on $n$ and $b$ . For example, for $n = 4$ ,

In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by $or, is equal to the binomial coefficient$

In mathematics, Stirling numbers arise in a variety of analytic and combinatorial problems. They are named after James Stirling, who introduced them in a purely algebraic setting in his book Methodus differentialis (1730). They were rediscovered and given a combinatorial meaning by Masanobu Saka in 1782.

In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.

In combinatorial mathematics, a derangement is a permutation of the elements of a set in which no element appears in its original position. In other words, a derangement is a permutation that has no fixed points.

In mathematics, the probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the result is of the prescribed kind is strictly greater than zero. Although the proof uses probability, the final conclusion is determined for certain, without any possible error.

In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Catalan.

In mathematics, summation is the addition of a sequence of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined.

In mathematics, a multiset is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist which contain only elements $a$ and $b$ , but vary in the multiplicities of their elements:

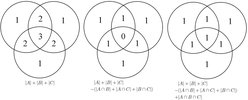
In combinatorics, a branch of mathematics, the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events. This inequality provides an upper bound on the probability of occurrence of at least one of a countable number of events in terms of the individual probabilities of the events. Boole's inequality is named for its discoverer, George Boole.

In mathematics, and in particular in group theory, a cyclic permutation is a permutation consisting of a single cycle. In some cases, cyclic permutations are referred to as cycles; if a cyclic permutation has k elements, it may be called a k-cycle. Some authors widen this definition to include permutations with fixed points in addition to at most one non-trivial cycle. In cycle notation, cyclic permutations are denoted by the list of their elements enclosed with parentheses, in the order to which they are permuted.

In proving results in combinatorics several useful combinatorial rules or combinatorial principles are commonly recognized and used.

<span class="mw-page-title-main">Rule of product</span> Basic counting principle in mathematics

In combinatorics, the rule of product or multiplication principle is a basic counting principle. Stated simply, it is the intuitive idea that if there are a ways of doing something and b ways of doing another thing, then there are a · b ways of performing both actions.

In mathematics, particularly in combinatorics, a Stirling number of the second kind is the number of ways to partition a set of n objects into k non-empty subsets and is denoted by $or . Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions. They are named after James Stirling.$

In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.

The Rand index or Rand measure in statistics, and in particular in data clustering, is a measure of the similarity between two data clusterings. A form of the Rand index may be defined that is adjusted for the chance grouping of elements, this is the adjusted Rand index. The Rand index is the accuracy of determining if a link belongs within a cluster or not.

In mathematics, in the field of combinatorics, the q-Vandermonde identity is a q-analogue of the Chu–Vandermonde identity. Using standard notation for q-binomial coefficients, the identity states that

References

1 2 3 Biggs 2002, p. 91.
1 2 3 4 5 mps (22 March 2013). "enumerative combinatorics". PlanetMath. Archived from the original on 23 July 2014. Retrieved 14 August 2021.
1 2 Leung, K. T.; Cheung, P. H. (1988-04-01). Fundamental Concepts of Mathematics. Hong Kong University Press. p. 66. ISBN 978-962-209-181-8.
↑ Penner, R. C. (1999). Discrete Mathematics: Proof Techniques and Mathematical Structures. World Scientific. p. 342. ISBN 978-981-02-4088-2.
↑ "4.1: Definition and Properties". Mathematics LibreTexts. 2021-08-24. Retrieved 2024-05-02.
↑ "Rule of sum and rule of product | Combinatorics | Discrete math | Math". Hyperskill. Retrieved 2024-05-02.
1 2 Biggs 2002, p. 112.
↑ Diedrichs, Danilo R. (2022). Transition to advanced mathematics. Stephen Lovett. Boca Raton, FL. p. 172. ISBN 978-1-003-04620-2. OCLC 1302331608.{{cite book}}: CS1 maint: location missing publisher (link)
1 2 Moreno, Miguel (2018). "Lecture notes: Combinatorics" (PDF). u.math.biu.ac.il. Archived (PDF) from the original on 19 August 2019. Retrieved 26 November 2022.
↑ Henry Adams; Kelly Emmrich; Maria Gillespie; Shannon Golden; Rachel Pries (15 November 2021). "Counting Rocks! An Introduction to Combinatorics". arXiv: 2108.04902 [math.HO].

Bibliography

Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. ISBN 978-0-19-871369-2.