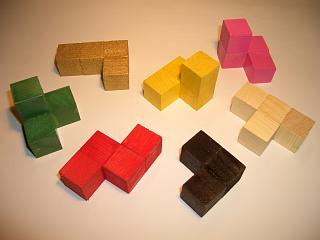The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. There are 92 solutions. The problem was first posed in the mid-19th century. In the modern era, it is often used as an example problem for various computer programming techniques.
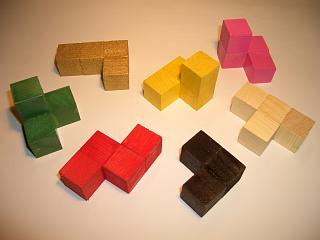
The Soma cube is a solid dissection puzzle invented by Danish polymath Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg.

The Tower of Hanoi is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical shape. The objective of the puzzle is to move the entire stack to one of the other rods, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- No disk may be placed on top of a disk that is smaller than it.
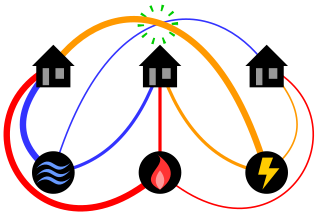
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.
Marilyn vos Savant is an American magazine columnist who has the highest recorded intelligence quotient (IQ) in the Guinness Book of Records, a competitive category the publication has since retired. Since 1986, she has written "Ask Marilyn", a Parade magazine Sunday column wherein she solves puzzles and answers questions on various subjects, and which popularized the Monty Hall problem in 1990.
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions. Mathematical puzzles require mathematics to solve them. Logic puzzles are a common type of mathematical puzzle.

The 15 puzzle is a sliding puzzle. It has 15 square tiles numbered 1 to 15 in a frame that is 4 tile positions high and 4 tile positions wide, with one unoccupied position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to place the tiles in numerical order.
Verbal arithmetic, also known as alphametics, cryptarithmetic, cryptarithm or word addition, is a type of mathematical game consisting of a mathematical equation among unknown numbers, whose digits are represented by letters of the alphabet. The goal is to identify the value of each letter. The name can be extended to puzzles that use non-alphabetic symbols instead of letters.

Kakuro or Kakkuro or Kakoro is a kind of logic puzzle that is often referred to as a mathematical transliteration of the crossword. Kakuro puzzles are regular features in many math-and-logic puzzle publications across the world. In 1966, Canadian Jacob E. Funk, an employee of Dell Magazines, came up with the original English name Cross Sums and other names such as Cross Addition have also been used, but the Japanese name Kakuro, abbreviation of Japanese kasan kurosu, seems to have gained general acceptance and the puzzles appear to be titled this way now in most publications. The popularity of Kakuro in Japan is immense, second only to Sudoku among Nikoli's famed logic-puzzle offerings.

The wolf, goat and cabbage problem is a river crossing puzzle. It dates back to at least the 9th century, and has entered the folklore of several cultures.
Lights Out is an electronic game released by Tiger Electronics in 1995. The game consists of a 5 by 5 grid of lights. When the game starts, a random number or a stored pattern of these lights is switched on. Pressing any of the lights will toggle it and the adjacent lights. The goal of the puzzle is to switch all the lights off, preferably with as few button presses as possible.

Sudoku is a logic-based, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.

Mathematics can be used to study Sudoku puzzles to answer questions such as "How many filled Sudoku grids are there?", "What is the minimal number of clues in a valid puzzle?" and "In what ways can Sudoku grids be symmetric?" through the use of combinatorics and group theory.

This is a glossary of Sudoku terms and jargon. Sudoku with a 9×9 grid is assumed, unless otherwise noted.
God's algorithm is a notion originating in discussions of ways to solve the Rubik's Cube puzzle, but which can also be applied to other combinatorial puzzles and mathematical games. It refers to any algorithm which produces a solution having the fewest possible moves. The allusion to the deity is based on the notion that an omniscient being would know an optimal step from any given configuration.
The 24 puzzle is an arithmetical puzzle in which the objective is to find a way to manipulate four integers so that the end result is 24. For example, for the numbers 4, 7, 8, 8, a possible solution is . Note that all four numbers must be used exactly once.
The Sum and Product Puzzle, also known as the Impossible Puzzle because it seems to lack sufficient information for a solution, is a logic puzzle. It was first published in 1969 by Hans Freudenthal, and the name Impossible Puzzle was coined by Martin Gardner. The puzzle is solvable, though not easily. There exist many similar puzzles.

The Eternity II puzzle is an edge-matching puzzle launched on 28 July 2007. It was developed by Christopher Monckton and marketed and copyrighted by TOMY UK Ltd as a successor to the original Eternity puzzle. The puzzle was part of a competition in which a $2 million prize was offered for the first complete solution. The competition ended at noon on 31 December 2010, with no solution being found.
A Tangled Tale is a collection of 10 brief humorous stories by Lewis Carroll, published serially between April 1880 and March 1885 in The Monthly Packet magazine. Arthur B. Frost added illustrations when the series was printed in book form. The stories, or Knots as Carroll calls them, present mathematical problems. In a later issue, Carroll gives the solution to a Knot and discusses readers' answers. The mathematical interpretations of the Knots are not always straightforward. The ribbing of readers answering wrongly – giving their names – was not always well received.
"Cheryl's Birthday" is a logic puzzle, specifically a knowledge puzzle. The objective is to determine the birthday of a girl named Cheryl using a handful of clues given to her friends Albert and Bernard. Written by Dr Joseph Yeo Boon Wooi of Singapore's National Institute of Education, the question was posed as part of the Singapore and Asian Schools Math Olympiad (SASMO) in 2015, and was first posted online by Singapore television presenter Kenneth Kong. It went viral in a matter of days and also hit national television in all major cities globally. Henry Ong, the Founder of SASMO was interviewed by Singapore's Mediacorp program FIVE hosts Chua En Lai and Yasmine Yonkers.