The Amott test is one of the most widely used empirical wettability measurements for reservoir cores in petroleum engineering. The method combines two spontaneous imbibition measurements and two forced displacement measurements. This test defines two different indices: the Amott water index () and the Amott oil index ().
The two Amott indices are often combined to give the Amott–Harvey index. It is a number between −1 and 1 describing wettability of a rock in drainage processes. It is defined as:
These two indices are obtained from special core analysis (SCAL) experiments (porous plate or centrifuge) by plotting the capillary pressure curve as a function of the water saturation as shown on figure 1:
with is the water saturation for a zero capillary pressure during the imbibition process, is the irreducible water saturation and is the residual oil saturation after imbibition.
with is the oil saturation for a zero capillary pressure during the secondary drainage process, is the irreducible water saturation and is the residual non-wetting phase saturation after imbibition.
A rock is defined as:
| Amott-Harvey index | ||
|---|---|---|
| Name | Lower bound | Upper bound |
| Oil wet | -1 | -0.3 |
| Weakly oil wet | -0.3 | 0 |
| Weakly water wet | 0 | 0.3 |
| Water wet | 0.3 | 1 |
In fluid mechanics, materials science and Earth sciences, permeability is a measure of the ability of a porous material to allow fluids to pass through it.
Darcy's law is an equation that describes the flow of a fluid through a porous medium and through a Hele-Shaw cell. The law was formulated by Henry Darcy based on results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences. It is analogous to Ohm's law in electrostatics, linearly relating the volume flow rate of the fluid to the hydraulic head difference via the hydraulic conductivity. In fact, the Darcy's law is a special case of the Stokes equation for the momentum flux, in turn deriving from the momentum Navier–Stokes equation.
In physics, Washburn's equation describes capillary flow in a bundle of parallel cylindrical tubes; it is extended with some issues also to imbibition into porous materials. The equation is named after Edward Wight Washburn; also known as Lucas–Washburn equation, considering that Richard Lucas wrote a similar paper three years earlier, or the Bell-Cameron-Lucas-Washburn equation, considering J.M. Bell and F.K. Cameron's discovery of the form of the equation in 1906.
Water content or moisture content is the quantity of water contained in a material, such as soil, rock, ceramics, crops, or wood. Water content is used in a wide range of scientific and technical areas, and is expressed as a ratio, which can range from 0 to the value of the materials' porosity at saturation. It can be given on a volumetric or mass (gravimetric) basis.
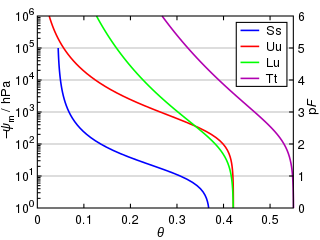
Water retention curve is the relationship between the water content, θ, and the soil water potential, ψ. The soil moisture curve is characteristic for different types of soil, and is also called the soil moisture characteristic.
In fluid statics, capillary pressure is the pressure between two immiscible fluids in a thin tube, resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as both an opposing or driving force for fluid transport and is a significant property for research and industrial purposes. It is also observed in natural phenomena.
In petrophysics, Archie's law is a purely empirical law relating the measured electrical conductivity of a porous rock to its porosity and fluid saturation. It is named after Gus Archie (1907–1978) and laid the foundation for modern well log interpretation, as it relates borehole electrical conductivity measurements to hydrocarbon saturations.
Petrophysics is the study of physical and chemical rock properties and their interactions with fluids.
Effective porosity is most commonly considered to represent the porosity of a rock or sediment available to contribute to fluid flow through the rock or sediment, or often in terms of "flow to a borehole". Porosity that is not considered "effective porosity" includes water bound to clay particles and isolated "vuggy" porosity. The effective porosity is of great importance in considering the suitability of rocks or sediments as oil or gas reservoirs, or as aquifers.
In multiphase flow in porous media, the relative permeability of a phase is a dimensionless measure of the effective permeability of that phase. It is the ratio of the effective permeability of that phase to the absolute permeability. It can be viewed as an adaptation of Darcy's law to multiphase flow.
In fluid dynamics, the Buckley–Leverett equation is a conservation equation used to model two-phase flow in porous media. The Buckley–Leverett equation or the Buckley–Leverett displacement describes an immiscible displacement process, such as the displacement of oil by water, in a one-dimensional or quasi-one-dimensional reservoir. This equation can be derived from the mass conservation equations of two-phase flow, under the assumptions listed below.
In petroleum engineering, the Leverett J-function is a dimensionless function of water saturation describing the capillary pressure,
The pore space of soil contains the liquid and gas phases of soil, i.e., everything but the solid phase that contains mainly minerals of varying sizes as well as organic compounds.
In materials science and biology, capillary condensation is the "process by which multilayer adsorption from the vapor [phase] into a porous medium proceeds to the point at which pore spaces become filled with condensed liquid from the vapor [phase]." The unique aspect of capillary condensation is that vapor condensation occurs below the saturation vapor pressure, Psat, of the pure liquid. This result is due to an increased number of van der Waals interactions between vapor phase molecules inside the confined space of a capillary. Once condensation has occurred, a meniscus immediately forms at the liquid-vapor interface which allows for equilibrium below the saturation vapor pressure. Meniscus formation is dependent on the surface tension of the liquid and the shape of the capillary, as shown by the Young-Laplace equation. As with any liquid-vapor interface involving a meniscus, the Kelvin equation provides a relation for the difference between the equilibrium vapor pressure and the saturation vapor pressure. A capillary does not necessarily have to be a tubular, closed shape, but can be any confined space with respect to its surroundings.
The black-oil equations are a set of partial differential equations that describe fluid flow in a petroleum reservoir, constituting the mathematical framework for a black-oil reservoir simulator. The term black-oil refers to the fluid model, in which water is modeled explicitly together with two hydrocarbon components, one (pseudo) oil phase and one (pseudo-)gas phase. This is in contrast with a compositional formulation, in which each hydrocarbon component is handled separately.
The rise in core (RIC) method is an alternate reservoir wettability characterization method described by S. Ghedan and C. H. Canbaz in 2014. The method enables estimation of all wetting regions such as strongly water wet, intermediate water, oil wet and strongly oil wet regions in relatively quick and accurate measurements in terms of Contact angle rather than wettability index.
Morris Muskat et al. developed the governing equations for multiphase flow in porous media as a generalisation of Darcy's equation for water flow in porous media. The porous media are usually sedimentary rocks such as clastic rocks or carbonate rocks.
In petroleum engineering, TEM, also called TEM-function is a criterion to characterize dynamic two-phase flow characteristics of rocks. TEM is a function of relative permeability, porosity, absolute permeability and fluid viscosity, and can be determined for each fluid phase separately. TEM-function has been derived from Darcy's law for multiphase flow.
In petroleum engineering, Lak wettability index is a quantitative indicator to measure wettability of rocks from relative permeability data. This index is based on a combination of Craig's first rule. and modified Craig's second rule
The U.S. Bureau of Mines (USBM), developed by Donaldson et al. in 1969, is a method to measure wettability of petroleum reservoir rocks. In this method, the areas under the forced displacement Capillary pressure curves of oil and water drive processes are denoted as and to calculate the USBM index.
 | This fluid dynamics–related article is a stub. You can help Wikipedia by expanding it. |
