Rise in core

Last updated June 23, 2024

The rise in core (RIC) method is an alternate reservoir wettability characterization method described by S. Ghedan and C. H. Canbaz in 2014. The method enables estimation of all wetting regions such as strongly water wet, intermediate water, oil wet and strongly oil wet regions in relatively quick and accurate measurements in terms of Contact angle rather than wettability index.

During the RIC experiments, core samples saturated with selected reservoir fluid were subjected to imbibition from a second reservoir fluid. RIC wettability measurements are compared with and modified – Amott test ^[1] and USBM measurements using core plug pairs from different heights of a thick carbonate reservoir. Results show good coherence. The RIC method is an alternate method to Amott and USBM methods and that efficiently characterizes Reservoir Wettability.^[2]^[3]

Cut-off values vs wettability index

One study used the water advancing contact angle to estimate the wettability of fifty-five oil reservoirs. De-oxygenated synthetic formation brine and dead anaerobic crude was tested on quartz and calcite crystals at reservoir temperature. Contact angles from 0 to 75 degrees were deemed water wet, 75 to 105 degrees as intermediate and 105 to 180 degrees as oil wet.^[4] Although the range of wettabilities were divided into three regions, these were arbitrary divisions. The wettability of different reservoirs can vary within the broad spectrum from strongly water-wet to strongly oil-wet.

Another study described two initial conditions as reference and non-reference for calculating cut-off values by using advancing and receding contact angles and spontaneous imbibition data.^[5] Limiting value between water wet and intermediate zones was described as 62-degree. Similarly, cut-off values for advancing contact angle is described as 0 to 62 degrees for water wet region, 62 to 133 degrees for Intermediate-wet zone, and 133 to 180 degrees for Oil wet zone. Chilingar and Yen^[6] examined extensive research work on 161 limestone, dolomitic limestone, calcitic dolomite, and dolomite cores. Cut-off values classified as 160 to 180 degrees for strongly oil wet, 100 to 160 degrees for oil wet, 80 to 100 degrees intermediate wet, 80 to 20 degrees water wet and 0 to 20 strongly water wet.

Rise in core uses a combination of Chilingar et al. and Morrow wettability cut-off criteria. The contact angle range 80 – 100 degrees indicate neutral-wetness, the range 100 – 133 degrees indicate slight-oil wetness, the range 133 – 160 degrees indicate oil-wetness while the range 160- 180 degrees indicate strongly oil-wetness. The range 62 – 80 degrees indicate slight water wetness, the range 20 – 62 degrees indicate, water-wetness, while the range 0 – 20 degrees indicate strong water-wetness.

Technique

RIC wettability characterization technique is based on a modified form of Washburn's equation (1921). The technique enables relatively quick and accurate measurements of wettability in terms of contact angle while requiring no complex equipment. The method is applicable for any set of reservoir fluids, on any type of reservoir rock and at any heterogeneity level. It characterizes wettability across the board from strongly water to strongly oil wet conditions.^[7]

The step of deriving the modified form of Washburn equation for a rock/liquid/liquid system involves acquiring a Washburn equation for a rock/air/liquid system. The Washburn equation for a rock/air/liquid system is represented by:

t={\mu  \over C\rho ^{2}\gamma \cos \theta }{m^{2}}

(Eq.1).

Herein, "t" is the penetration rate of liquid into a porous sample, "μ" is the liquid's viscosity, "ρ" is the liquid's density, "γ" is the liquid's surface tension, "θ" is the liquid's contact angle, "m" is the mass of the liquid that penetrates the porous sample and "C" is the constant of characterization of the porous sample. evaluating a value of "γ_os" using a young’s equation for a rock surface/water/air system (Figure 2) and a value of "γ_ws" using young’s equation for a liquid/liquid/rock system is represented as:

\gamma _{ow}\cos \theta =\gamma _{os}\gamma _{ws}

(Eq.2).

"γ_ow" is the surface tension between the oil and water system, "γ_os" is the surface tension between oil and solid system and "γ_ws" is the surface tension between water and the solid system. Using Young's equation for a rock surface/ water/air system and substituting in equation (2) to obtain equation 3:

\cos \theta _{wo}={{\gamma _{o}\cos \theta _{o}}\cdot {\gamma _{w}\cos \theta _{w}} \over {\gamma _{wo}}}

(Eq. 3).

Rearranging equation (1) to factor out γ_LV obtains equation (4), wherein γ_LV a liquid-vapor surface tension is:

\gamma _{LV}={\mu  \over C\rho ^{2}\gamma \cos \theta }\cdot {m^{2} \over t}

(Eq. 4).

Realizing that γ_LV (liquid–vapor surface tension) is equivalent to γ_o (oil–air surface tension), or γ_w (water–air-surface tension), substituting equation (4) in equation (3) and cancelling out similar terms obtains equation (5):

\cos \theta _{wo}={{({{m^{2}\mu _{o}} \over {C{\rho _{o}}^{2}t}})-({{m^{2}\mu _{w}} \over {C{\rho _{w}}^{2}t}})} \over \mu _{wo}}

(Eq. 5).

Therein, γ_LV is liquid-vapor surface tension, γ_ois oil-air surface tension, γ_w is water-air surface tension, μ_o is viscosity of oil and μ_w is viscosity of water. cosθ_wo is contact angle between water and oil; representing a relationship between a mass of water imbibed into the core sample and a mass of oil imbibed in the core sample with an equation (6):

{\rho _{w}gV_{w}}={\rho _{o}gV_{o}}

(Eq. 6).

Therein ρ_w is density of water and V_w is volume of water imbibed, ρ_o is density of oil and V_o is volume of oil imbibed, the amount of water imbibed and amount of oil imbibed under gravity are same; and air behaves as a strong non-wetting phase in both an oil–air–solid and a water–air–solid systems, thereby indicating that both oil and water behave as strong wetting phases, resulting in equal air/oil and air/water capillary forces for the same porous media and for a given pore size distribution. Thus, a mass change of a core sample due to water imbibition is equal to a mass change of a core sample due to oil imbibition, because water or oil penetration of the porous media at any time is a function of a balance between gravity and capillary forces. The mass of water imbibed into a core sample is approximately equal to a mass of oil imbibed in the core sample core samples of a same rock type and dimensions, and for equal capillary forces;

Cancelling out g in equation(6) gives equation (7):

{\rho _{w}V_{w}}={\rho _{o}V_{o}}

(Eq. 7),

which means

{m_{w}}={m_{o}}

(Eq. 8).

Therein, m_w is mass of water and m_o is mass of oil. Factoring out $C{m^{2} \over t}$ from Eq. 5 to obtain Eq. 9, gives Modified Washburn Equation:

{\cos \theta _{12}}={{{{(\mu _{1}{\rho _{2}}^{2})}-{(\mu _{2}{\rho _{1}}^{2})}} \over {{{\rho _{1}}^{2}}{{\rho _{2}}^{2}}C\mu _{L1L2}}}\cdot \left({m^{2} \over t}\right)}

(Eq. 9).

Therein θ₁₂ is the contact angle of liquid/liquid/rock system, μ₁ is a viscosity of oil phase, μ₂ is a viscosity of water phase, ρ₁ is density of oil phase in g/cm³, ρ₂ is density of water phase in g/cm³, m is mass of fluid penetrated into a porous rock, t is time in min, γ__L1L2 is the surface tension between an oil and a water in dyne/cm, and ∁ is a characteristic constant of the porous rock.

Figure 1 RIC Experimental Setup.jpg — Figure 1

Experimental setup and procedure

Schematic view and experimental setups of the RIC wettability testing method is described in Figure 1. Core plugs are divided into 3–4 core samples, each of 3.8 cm average diameter and 1.5 cm length. The lateral area of each core sample is sealed by epoxy resin to ensure one-dimensional liquid penetration into the core by imbibition. A hook is mounted on top side of the core sample.

The RIC setup includes a beaker to host the imbibing fluid. A thin rope connects the core sample to a high-precision balance (0.001 gm accurate). A hanging core sample is positioned with the bottom part of the sample barely touching the imbibing fluid in the beaker. Relative saturation as well as mass of core samples starts to change during imbibition. A computer connected to a balance continuously monitors the core sample mass change over time. Plots of squared mass change versus time are generated.^[2]^[8]

Determination of "C" constant

The RIC experiment is first performed with a n-dodecane–air–rock system to determine the constant ∁ of the Washburn Equation. N-dodecane imbibes into one of the core samples and the imbibition curve is recorded in Figure 2. Dodecane is an alkane that has low surface energy, very strongly wetting the rock sample in the presence of air, with contact angle θ equal to zero. Constant ∁ is determined by the contact angle value for dodecane/air/rock system, determining physical properties of n-dodecane (ρ,μ,γ) and rearranging equation 1;

C={\mu  \over \rho ^{2}\gamma _{LV}\cos \theta }\cdot {m^{2} \over t}

(Eq. 10)

Experiment

The second step of the RIC experimental process is to saturate the neighboring core sample with crude oil and subjected the sample to water imbibition. Applying the slope of the RIC curve $({m^{2} \over t})$ , fluid properties of oil/brine system (ρ,μ,γ) and the ∁ value are determined from the neighboring core sample into Eq. 9 to calculate the contact angle, θ.

Related Research Articles

<span class="mw-page-title-main">Surface tension</span> Tendency of a liquid surface to shrink to reduce surface area

Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects to float on a water surface without becoming even partly submerged.

In gas dynamics, Chaplygin's equation, named after Sergei Alekseevich Chaplygin (1902), is a partial differential equation useful in the study of transonic flow. It is

In physics, Washburn's equation describes capillary flow in a bundle of parallel cylindrical tubes; it is extended with some issues also to imbibition into porous materials. The equation is named after Edward Wight Washburn; also known as Lucas–Washburn equation, considering that Richard Lucas wrote a similar paper three years earlier, or the Bell-Cameron-Lucas-Washburn equation, considering J.M. Bell and F.K. Cameron's discovery of the form of the equation in 1906.

Wetting is the ability of a liquid to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. This happens in presence of a gaseous phase or another liquid phase not miscible with the first one. The degree of wetting (wettability) is determined by a force balance between adhesive and cohesive forces. There are two types of wetting: non-reactive wetting and reactive wetting.

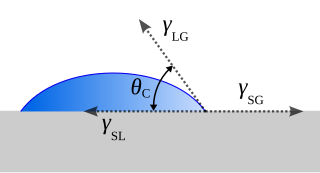
The contact angle is the angle between a liquid surface and a solid surface where they meet. More specifically, it is the angle between the surface tangent on the liquid–vapor interface and the tangent on the solid–liquid interface at their intersection. It quantifies the wettability of a solid surface by a liquid via the Young equation.

Cassie's law, or the Cassie equation, describes the effective contact angle θ_c for a liquid on a chemically heterogeneous surface, i.e. the surface of a composite material consisting of different chemistries, that is, non-uniform throughout. Contact angles are important as they quantify a surface's wettability, the nature of solid-fluid intermolecular interactions. Cassie's law is reserved for when a liquid completely covers both smooth and rough heterogeneous surfaces.

In fluid statics, capillary pressure is the pressure between two immiscible fluids in a thin tube, resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as both an opposing or driving force for fluid transport and is a significant property for research and industrial purposes. It is also observed in natural phenomena.

In physics, the Young–Laplace equation is an algebraic equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension or wall tension, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface :

A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca⁺ and Sr⁺ and other ions such as He⁺, Li²⁺, and Be³⁺ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.

The capillary length or capillary constant is a length scaling factor that relates gravity and surface tension. It is a fundamental physical property that governs the behavior of menisci, and is found when body forces (gravity) and surface forces are in equilibrium.

In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.

In general relativity, a point mass deflects a light ray with impact parameter $by an angle approximately equal to$

Nuclear magnetic resonance (NMR) in porous materials covers the application of using NMR as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity and pore size distribution, the permeability, the water saturation, the wettability, etc.

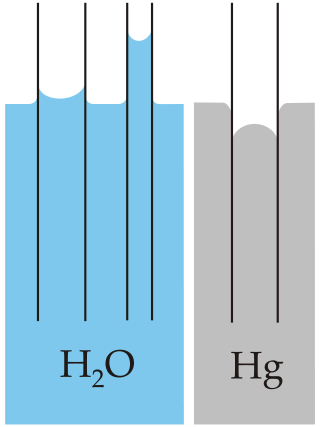
<span class="mw-page-title-main">Jurin's law</span>

Jurin's law, or capillary rise, is the simplest analysis of capillary action—the induced motion of liquids in small channels—and states that the maximum height of a liquid in a capillary tube is inversely proportional to the tube's diameter. Capillary action is one of the most common fluid mechanical effects explored in the field of microfluidics. Jurin's law is named after James Jurin, who discovered it between 1718 and 1719. His quantitative law suggests that the maximum height of liquid in a capillary tube is inversely proportional to the tube's diameter. The difference in height between the surroundings of the tube and the inside, as well as the shape of the meniscus, are caused by capillary action. The mathematical expression of this law can be derived directly from hydrostatic principles and the Young–Laplace equation. Jurin's law allows the measurement of the surface tension of a liquid and can be used to derive the capillary length.

In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.

In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.

In physics, the distorted Schwarzschild metric is the metric of a standard/isolated Schwarzschild spacetime exposed in external fields. In numerical simulation, the Schwarzschild metric can be distorted by almost arbitrary kinds of external energy–momentum distribution. However, in exact analysis, the mature method to distort the standard Schwarzschild metric is restricted to the framework of Weyl metrics.

Morris Muskat et al. developed the governing equations for multiphase flow in porous media as a generalisation of Darcy's equation for water flow in porous media. The porous media are usually sedimentary rocks such as clastic rocks or carbonate rocks.

In fluid mechanics, the thin-film equation is a partial differential equation that approximately predicts the time evolution of the thickness $h$ of a liquid film that lies on a surface. The equation is derived via lubrication theory which is based on the assumption that the length-scales in the surface directions are significantly larger than in the direction normal to the surface. In the non-dimensional form of the Navier-Stokes equation the requirement is that terms of order $ε 2$ and $ε 2 Re$ are negligible, where $ε ≪ 1$ is the aspect ratio and $Re$ is the Reynolds number. This significantly simplifies the governing equations. However, lubrication theory, as the name suggests, is typically derived for flow between two solid surfaces, hence the liquid forms a lubricating layer. The thin-film equation holds when there is a single free surface. With two free surfaces, the flow must be treated as a viscous sheet.

In fluid dynamics, Landau–Squire jet or Submerged Landau jet describes a round submerged jet issued from a point source of momentum into an infinite fluid medium of the same kind. This is an exact solution to the incompressible form of the Navier-Stokes equations, which was first discovered by Lev Landau in 1944 and later by Herbert Squire in 1951. The self-similar equation was in fact first derived by N. A. Slezkin in 1934, but never applied to the jet. Following Landau's work, V. I. Yatseyev obtained the general solution of the equation in 1950.

References

↑ Amott, E. (1959). Observations related to Wettability of Porous Rock. AIME. pp. 216, 156–162.
1 2 Ghedan, Shawket G.; Canbaz, Celal Hakan (19 January 2014). Theory and Experimental Setup of the New Rise in Core Reservoir Wettability Measurement Technique. doi:10.2523/iptc-17659-ms. ISBN 9781613993224.
↑ US patent 20120136578
↑ Treiber, L.E.; Owens, W.W. (1 December 1972). "A Laboratory Evaluation of the Wettability of Fifty Oil-Producing Reservoirs". Society of Petroleum Engineers Journal. 12 (6): 531–540. doi:10.2118/3526-pa. ISSN 0197-7520.
↑ Ma, S.M.; Zhang, X.; Morrow, N.R.; Zhou, X. (1 December 1999). "Characterization of Wettability From Spontaneous Imbibition Measurements". Journal of Canadian Petroleum Technology. 38 (13): 49. Bibcode:1999BCaPG..38.1349M. doi:10.2118/99-13-49. ISSN 0021-9487.
↑ Chilingar, George V.; Yen, T. F. (1 January 1983). "Some Notes on Wettability and Relative Permeabilities of Carbonate Reservoir Rocks, II". Energy Sources. 7 (1): 67–75. doi:10.1080/00908318308908076. ISSN 0090-8312.
↑ Ghedan, Shawkat G.; Canbaz, Celal Hakan; Boyd, Douglas A.; Mani, George M.; Haggag, Marwan Khamis (1 January 2010). "Wettability Profile of a Thick Carbonate Reservoir by the New Rise in Core Wettability Characterization Method". All Days. doi:10.2118/138697-ms. ISBN 9781555633158.{{cite book}}: |journal= ignored (help)
↑ Canbaz, C.H., Ghedan, S.G., "Theory and Experimental Setup of the New Rise in Core Reservoir Wettability Measurement Technique" IPTC #17659, IPTC, Doha, Qatar, January 2014.

Brown, Jeffrey S. (31 December 2013). Compositional simulation model for carbon dioxide flooding with improved fluid trapping, A. Colorado School of Mines (Thesis).
Luo, Peng; Li, Sheng (2017). "Simultaneous Capillary Pressure and Wettability Determination for Tight Bakken Cores Using an Ultra-High-Speed Centrifuge". SPE Unconventional Resources Conference. doi:10.2118/185067-MS.
Klewiah, Isaac (30 July 2018). Adsorption of Polar Oil Components onto Chalk: Impact of Silica content on Initial Wetting. University of Stavanger (Master thesis).
Smajla, Ivan (21 September 2017). Usporedba različitih metoda analiza močivosti i relativnih propusnosti stijena i njihov utjecaj na iscrpak ugljikovodika iz novog naftnog ležišta u Savskoj depresiji. Croatian Digital Theses Repository (info:eu-repo/semantics/masterThesis).
Seid Mohammadi, M.; Moghadasi, J.; Naseri, S. (2014). "An experimental investigation of wettability alteration in carbonate reservoir using γ-Al2O3 nanoparticles". Iranian Journal of Oil & Gas Science and Technology. 3 (2): 18–26. doi:10.22050/ijogst.2014.6034. S2CID 128535266.
Bassioni, Ghada; Taha Taqvi, Syed (2015). "Wettability Studies Using Zeta Potential Measurements". Journal of Chemistry. 2015: 1–6. doi: 10.1155/2015/743179 . S2CID 73527516.
Sprunt, E. S.; Collins, S. H. (1991). "U.S. Patent No. 5,069,065". Washington, DC: U.S. Patent and Trademark Office.
Taqvi, Syed Taha; Almansoori, Ali; Bassioni, Ghada (2016). "Understanding the Role of Asphaltene in Wettability Alteration Using ζ Potential Measurements". Energy Fuels. 30 (3): 1927–1932. doi:10.1021/acs.energyfuels.5b02127.
c. Ferreira, Flavio; Stukan, Mikhail; Liang, Lin; Souza, Andre; Venkataramanan, Lalitha; Beletskaya, Anna; Dias, Daniel; Dantas Da Silva, Marianna (2018). "New Model for Wettability Change with Depth in Mixed-Wet Complex Carbonates". Abu Dhabi International Petroleum Exhibition & Conference. doi:10.2118/192758-MS. S2CID 140061917.
Seiedi, Omolbanin; Zahedzadeh, Mohammad; Roayaei, Emad; Aminnaji, Morteza; Fazeli, Hossein (2020). "Experimental and modeling study of wettability alteration through seawater injection in limestone: a case study". Petroleum Science. 17 (3): 749–758. Bibcode:2020PetSc..17..749S. doi: 10.1007/s12182-019-00407-y .
"Rise in core wettability characterization method".
Canbaz, C. H.; Ghedan, S. (2015). "Wettability characterization of different oil/brine/rock systems by using Rise in Core method". 20th international petroleum and natural gas congress and exhibition (IPETGAS). Turkey. pp. 365–370.{{cite book}}: CS1 maint: location missing publisher (link)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Amott, E. (1959). Observations related to Wettability of Porous Rock. AIME. pp. 216, 156–162.

[:1-2] 1 2 Ghedan, Shawket G.; Canbaz, Celal Hakan (19 January 2014). Theory and Experimental Setup of the New Rise in Core Reservoir Wettability Measurement Technique. doi:10.2523/iptc-17659-ms. ISBN 9781613993224.

[3] US patent 20120136578

[4] Treiber, L.E.; Owens, W.W. (1 December 1972). "A Laboratory Evaluation of the Wettability of Fifty Oil-Producing Reservoirs". Society of Petroleum Engineers Journal. 12 (6): 531–540. doi:10.2118/3526-pa. ISSN 0197-7520.

[5] Ma, S.M.; Zhang, X.; Morrow, N.R.; Zhou, X. (1 December 1999). "Characterization of Wettability From Spontaneous Imbibition Measurements". Journal of Canadian Petroleum Technology. 38 (13): 49. Bibcode:1999BCaPG..38.1349M. doi:10.2118/99-13-49. ISSN 0021-9487.

[6] Chilingar, George V.; Yen, T. F. (1 January 1983). "Some Notes on Wettability and Relative Permeabilities of Carbonate Reservoir Rocks, II". Energy Sources. 7 (1): 67–75. doi:10.1080/00908318308908076. ISSN 0090-8312.

[7] Ghedan, Shawkat G.; Canbaz, Celal Hakan; Boyd, Douglas A.; Mani, George M.; Haggag, Marwan Khamis (1 January 2010). "Wettability Profile of a Thick Carbonate Reservoir by the New Rise in Core Wettability Characterization Method". All Days. doi:10.2118/138697-ms. ISBN 9781555633158.{{cite book}}: |journal= ignored (help)

[:0-8] Canbaz, C.H., Ghedan, S.G., "Theory and Experimental Setup of the New Rise in Core Reservoir Wettability Measurement Technique" IPTC #17659, IPTC, Doha, Qatar, January 2014.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]