
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect at exactly one point.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.
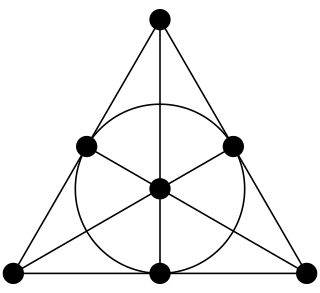
In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here, PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.
In projective geometry, duality or plane duality is a formalization of the striking symmetry of the roles played by points and lines in the definitions and theorems of projective planes. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.
In geometry, an affine plane is a system of points and lines that satisfy the following axioms:
An oval is a closed curve in a plane which resembles the outline of an egg. The term is not very specific, but in some areas it is given a more precise definition, which may include either one or two axes of symmetry of an ellipse. In common English, the term is used in a broader sense: any shape which reminds one of an egg. The three-dimensional version of an oval is called an ovoid.
In mathematics, a translation plane is a projective plane which admits a certain group of symmetries. Along with the Hughes planes and the Figueroa planes, translation planes are among the most well-studied of the known non-Desarguesian planes, and the vast majority of known non-Desarguesian planes are either translation planes, or can be obtained from a translation plane via successive iterations of dualization and/or derivation.

In projective geometry an oval is a point set in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.

In projective geometry an ovoid is a sphere like pointset (surface) in a projective space of dimension d ≥ 3. Simple examples in a real projective space are hyperspheres (quadrics). The essential geometric properties of an ovoid are:
- Any line intersects in at most 2 points,
- The tangents at a point cover a hyperplane, and
- contains no lines.
A maximal arc in a finite projective plane is a largest possible (k,d)-arc in that projective plane. If the finite projective plane has order q (there are q+1 points on any line), then for a maximal arc, k, the number of points of the arc, is the maximum possible (= qd + d - q) with the property that no d+1 points of the arc lie on the same line.
In mathematics, a non-Desarguesian plane is a projective plane that does not satisfy Desargues' theorem, or in other words a plane that is not a Desarguesian plane. The theorem of Desargues is true in all projective spaces of dimension not 2; in other words, the only projective spaces of dimension not equal to 2 are the classical projective geometries over a field. However, David Hilbert found that some projective planes do not satisfy it. The current state of knowledge of these examples is not complete.

Galois geometry is the branch of finite geometry that is concerned with algebraic and analytic geometry over a finite field. More narrowly, a Galois geometry may be defined as a projective space over a finite field.
In mathematics, a Hall plane is a non-Desarguesian projective plane constructed by Marshall Hall Jr. (1943). There are examples of order p2n for every prime p and every positive integer n provided p2n > 4.
In mathematics, a quadratic set is a set of points in a projective space that bears the same essential incidence properties as a quadric.
In geometry, specifically projective geometry, a blocking set is a set of points in a projective plane that every line intersects and that does not contain an entire line. The concept can be generalized in several ways. Instead of talking about points and lines, one could deal with n-dimensional subspaces and m-dimensional subspaces, or even more generally, objects of type 1 and objects of type 2 when some concept of intersection makes sense for these objects. A second way to generalize would be to move into more abstract settings than projective geometry. One can define a blocking set of a hypergraph as a set that meets all edges of the hypergraph.
In geometry, a unital is a set of n3 + 1 points arranged into subsets of size n + 1 so that every pair of distinct points of the set are contained in exactly one subset. This is equivalent to saying that a unital is a 2-(n3 + 1, n + 1, 1) block design. Some unitals may be embedded in a projective plane of order n2 (the subsets of the design become sets of collinear points in the projective plane). In this case of embedded unitals, every line of the plane intersects the unital in either 1 or n + 1 points. In the Desarguesian planes, PG(2,q2), the classical examples of unitals are given by nondegenerate Hermitian curves. There are also many non-classical examples. The first and the only known unital with non prime power parameters, n=6, was constructed by Bhaskar Bagchi and Sunanda Bagchi. It is still unknown if this unital can be embedded in a projective plane of order 36, if such a plane exists.
In projective geometry, a von Staudt conic is the point set defined by all the absolute points of a polarity that has absolute points. In the real projective plane a von Staudt conic is a conic section in the usual sense. In more general projective planes this is not always the case. Karl Georg Christian von Staudt introduced this definition in Geometrie der Lage (1847) as part of his attempt to remove all metrical concepts from projective geometry.

In projective geometry, Segre's theorem, named after the Italian mathematician Beniamino Segre, is the statement:

In projective geometry, Qvist's theorem, named after the Finnish mathematician Bertil Qvist, is a statement on ovals in finite projective planes. Standard examples of ovals are non-degenerate (projective) conic sections. The theorem gives an answer to the question How many tangents to an oval can pass through a point in a finite projective plane? The answer depends essentially upon the order of the plane.
A frequently studied problem in finite geometry is to identify ways in which an object can be covered by other simpler objects such as points, lines, and planes. In projective geometry, a specific instance of this problem that has numerous applications is determining whether, and how, a projective space can be covered by pairwise disjoint subspaces which have the same dimension; such a partition is called a spread. Specifically, a spread of a projective space , where is an integer and a division ring, is a set of -dimensional subspaces, for some such that every point of the space lies in exactly one of the elements of the spread.







