Related Research Articles

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.

Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.

An L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some larger string of symbols, an initial "axiom" string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. L-systems were introduced and developed in 1968 by Aristid Lindenmayer, a Hungarian theoretical biologist and botanist at the University of Utrecht. Lindenmayer used L-systems to describe the behaviour of plant cells and to model the growth processes of plant development. L-systems have also been used to model the morphology of a variety of organisms and can be used to generate self-similar fractals.
Parsing, syntax analysis, or syntactic analysis is the process of analyzing a string of symbols, either in natural language, computer languages or data structures, conforming to the rules of a formal grammar. The term parsing comes from Latin pars (orationis), meaning part.
In programming language theory, semantics is the rigorous mathematical study of the meaning of programming languages. Semantics assigns computational meaning to valid strings in a programming language syntax.
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain. The pushout consists of an object P along with two morphisms X → P and Y → P that complete a commutative square with the two given morphisms f and g. In fact, the defining universal property of the pushout essentially says that the pushout is the "most general" way to complete this commutative square. Common notations for the pushout are and .
In computer science, an abstract semantic graph (ASG) or term graph is a form of abstract syntax in which an expression of a formal or programming language is represented by a graph whose vertices are the expression's subterms. An ASG is at a higher level of abstraction than an abstract syntax tree, which is used to express the syntactic structure of an expression or program.
In computer science, graph transformation, or graph rewriting, concerns the technique of creating a new graph out of an original graph algorithmically. It has numerous applications, ranging from software engineering to layout algorithms and picture generation.
GXL is designed to be a standard exchange format for graphs. GXL is an extensible markup language (XML) sublanguage and the syntax is given by an XML document type definition (DTD). This exchange format offers an adaptable and flexible means to support interoperability between graph-based tools.
In theoretical computer science and mathematics, especially in the area of combinatorics on words, the Levi lemma states that, for all strings u, v, x and y, if uv = xy, then there exists a string w such that either
In mathematics and computer science, trace theory aims to provide a concrete mathematical underpinning for the study of concurrent computation and process calculi. The underpinning is provided by an algebraic definition of the free partially commutative monoid or trace monoid, or equivalently, the history monoid, which provides a concrete algebraic foundation, analogous to the way that the free monoid provides the underpinning for formal languages.
In computer programming, feature-oriented programming (FOP) or feature-oriented software development (FOSD) is a programming paradigm for program generation in software product lines (SPLs) and for incremental development of programs.
In mathematics, especially (higher) category theory, higher-dimensional algebra is the study of categorified structures. It has applications in nonabelian algebraic topology, and generalizes abstract algebra.
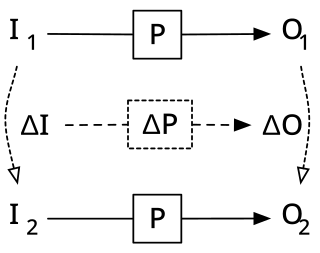
Incremental computing, also known as incremental computation, is a software feature which, whenever a piece of data changes, attempts to save time by only recomputing those outputs which depend on the changed data. When incremental computing is successful, it can be significantly faster than computing new outputs naively. For example, a spreadsheet software package might use incremental computation in its recalculation feature, to update only those cells containing formulas which depend on the changed cells.

Grzegorz Rozenberg is a Polish and Dutch computer scientist.
In computer science, double pushout graph rewriting refers to a mathematical framework for graph rewriting. It was introduced as one of the first algebraic approaches to graph rewriting in the article "Graph-grammars: An algebraic approach" (1973). It has since been generalized to allow rewriting structures which are not graphs, and to handle negative application conditions, among other extensions.
A term graph is a representation of an expression in a formal language as a generalized graph whose vertices are terms. Term graphs are a more powerful form of representation than expression trees because they can represent not only common subexpressions but also cyclic/recursive subexpressions.
Hans-Jörg Kreowski is a professor for computer science at the University of Bremen in North West Germany. His primary research area is theoretical computer science with an emphasis on graph transformation, algebraic specification, and syntactic picture processing. He is also a member of the Forum of Computer Scientists for Peace and Social Responsibility (FIfF).
In computer science, a single pushout graph rewriting or SPO graph rewriting refers to a mathematical framework for graph rewriting, and is used in contrast to the double-pushout approach of graph rewriting.
Hartmut Ehrig was a German computer scientist and professor of theoretical computer science and formal specification. He was a pioneer in algebraic specification of abstract data types, and in graph grammars.
References
- Rozenberg, Grzegorz (1997), Handbook of Graph Grammars and Computing by Graph Transformations, World Scientific Publishing, volumes 1–3, ISBN 9810228848 .
- Ehrig, Heckel, Korff, Lowe, Ribeiro, Wagner and Corradini, 1997. Algebraic Approaches to Graph Transformation - Part II: Single Pushout Approach and Comparison with Double Pushout Approach. Pp. 247-312 of (Rozenberg, 1997).