In graph theory, a b-coloring of a graph is a coloring of the vertices where each color class contains a vertex that has a neighbor in all other color classes.
The b-chromatic number of a G graph is the largest b(G) positive integer that the G graph has a b-coloring with b(G) number of colors.
Victor Campos, Carlos Lima és Ana Silva [1] used the relation between b-coloring and a graph's smallest cycle to partly prove the Erdős–Faber–Lovász conjecture.
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.
In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.
In graph theory, a critical graph is a graph G in which every vertex or edge is a critical element, that is, if its deletion decreases the chromatic number of G. Such a decrease cannot be by more than 1.
In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor.
In graph theory, complete coloring is the opposite of harmonious coloring in the sense that it is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic number ψ(G) of a graph G is the maximum number of colors possible in any complete coloring of G.
In graph theory, the Hadwiger conjecture states that if G is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree Δ of the graph. At least Δ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which Δ colors suffice, and "class two" graphs for which Δ + 1 colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most Δ+µ colors, where µ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.
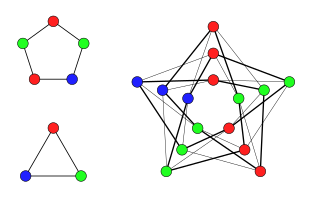
In graph theory, Hedetniemi's conjecture, formulated by Stephen T. Hedetniemi in 1966, concerns the connection between graph coloring and the tensor product of graphs. This conjecture states that
In graph theory, a nowhere-zero flow or NZ flow is a network flow that is nowhere zero. It is intimately connected to coloring planar graphs.
In graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a connected graph in which every vertex has at most Δ neighbors, the vertices can be colored with only Δ colors, except for two cases, complete graphs and cycle graphs of odd length, which require Δ + 1 colors.
In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not in general use the minimum number of colors possible.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős (1951), after whom it is named.
In graph theory, a mathematical discipline, coloring refers to an assignment of colours or labels to vertices, edges and faces of a graph. Defective coloring is a variant of proper vertex coloring. In a proper vertex coloring, the vertices are coloured such that no adjacent vertices have the same colour. In defective coloring, on the other hand, vertices are allowed to have neighbours of the same colour to a certain extent.
In graph theory, a total coloring is a coloring on the vertices and edges of a graph such that:
In graph theory, interval edge coloring is a type of edge coloring in which edges are labeled by the integers in some interval, every integer in the interval is used by at least one edge, and at each vertex the labels that appear on incident edges form a consecutive set of distinct numbers.