In combinatorial mathematics, Baranyai's theorem (proved by and named after Zsolt Baranyai) deals with the decompositions of complete hypergraphs.

In combinatorial mathematics, Baranyai's theorem (proved by and named after Zsolt Baranyai) deals with the decompositions of complete hypergraphs.
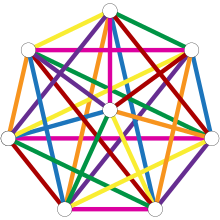
The statement of the result is that if are integers and r divides k, then the complete hypergraph decomposes into 1-factors. is a hypergraph with k vertices, in which every subset of r vertices forms a hyperedge; a 1-factor of this hypergraph is a set of hyperedges that touches each vertex exactly once, or equivalently a partition of the vertices into subsets of size r. Thus, the theorem states that the k vertices of the hypergraph may be partitioned into subsets of r vertices in different ways, in such a way that each r-element subset appears in exactly one of the partitions.
In the special case , we have a complete graph on vertices, and we wish to color the edges with colors so that the edges of each color form a perfect matching. Baranyai's theorem says that we can do this whenever is even.
The r = 2 case can be rephrased as stating that every complete graph with an even number of vertices has an edge coloring whose number of colors equals its degree, or equivalently that its edges may be partitioned into perfect matchings. It may be used to schedule round-robin tournaments, and its solution was already known in the 19th century. The case that k = 2r is also easy.
The r = 3 case was established by R. Peltesohn in 1936. The general case was proved by Zsolt Baranyai in 1975.
In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem states that, in any finite partially ordered set, the maximum size of an antichain of incomparable elements equals the minimum number of chains needed to cover all elements. This number is called the width of the partially order. The theorem is named for the mathematician Robert P. Dilworth, who published it in 1950.
In extremal graph theory, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem to bound the number of edges in an H-free graph for a non-complete graph H. It is named after Paul Erdős and Arthur Stone, who proved it in 1946, and it has been described as the “fundamental theorem of extremal graph theory”.
Discrepancy of hypergraphs is an area of discrepancy theory that studies the discrepancy of general set systems.

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.
In extremal graph theory, the forbidden subgraph problem is the following problem: given a graph , find the maximal number of edges an -vertex graph can have such that it does not have a subgraph isomorphic to . In this context, is called a forbidden subgraph.
In the mathematical discipline of graph theory, a rainbow matching in an edge-colored graph is a matching in which all the edges have distinct colors.
In graph theory, the hypergraph removal lemma states that when a hypergraph contains few copies of a given sub-hypergraph, then all of the copies can be eliminated by removing a small number of hyperedges. It is a generalization of the graph removal lemma. The special case in which the graph is a tetrahedron is known as the tetrahedron removal lemma. It was first proved by Nagle, Rödl, Schacht and Skokan and, independently, by Gowers.
In graph theory, a matching in a hypergraph is a set of hyperedges, in which every two hyperedges are disjoint. It is an extension of the notion of matching in a graph.
In graph theory, a vertex cover in a hypergraph is a set of vertices, such that every hyperedge of the hypergraph contains at least one vertex of that set. It is an extension of the notion of vertex cover in a graph.
In graph theory, the term bipartite hypergraph describes several related classes of hypergraphs, all of which are natural generalizations of a bipartite graph.
In the mathematical field of graph theory, Hall-type theorems for hypergraphs are several generalizations of Hall's marriage theorem from graphs to hypergraphs. Such theorems were proved by Ofra Kessler, Ron Aharoni, Penny Haxell, Roy Meshulam, and others.
In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.
In graph theory, Ryser's conjecture is a conjecture relating the maximum matching size and the minimum transversal size in hypergraphs.
In graph theory, perfect matching in high-degree hypergraphs is a research avenue trying to find sufficient conditions for existence of a perfect matching in a hypergraph, based only on the degree of vertices or subsets of them.
In mathematics, the hypergraph regularity method is a powerful tool in extremal graph theory that refers to the combined application of the hypergraph regularity lemma and the associated counting lemma. It is a generalization of the graph regularity method, which refers to the use of Szemerédi's regularity and counting lemmas.
{{citation}}: CS1 maint: location missing publisher (link).