Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory. He was awarded the Fields Medal in 1950.
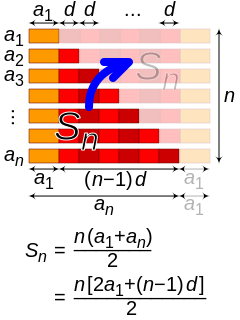
In number theory, an arithmetic, arithmetical, or number-theoretic function is for most authors any function f(n) whose domain is the positive integers and whose range is a subset of the complex numbers. Hardy & Wright include in their definition the requirement that an arithmetical function "expresses some arithmetical property of n".
In number theory, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.
Blum Blum Shub (B.B.S.) is a pseudorandom number generator proposed in 1986 by Lenore Blum, Manuel Blum and Michael Shub that is derived from Michael O. Rabin's one-way function.
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization, formulated in 1994. Informally, it solves the following problem: Given an integer , find its prime factors.
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case.
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of . Dirichlet characters are used to define Dirichlet L-functions, which are meromorphic functions with a variety of interesting analytic properties. If is a Dirichlet character, one defines its Dirichlet L-series by

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.

In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proven by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.

In number theory, the Carmichael function associates to every positive integer n a positive integer , defined as the smallest positive integer m such that
In analytic number theory, the Siegel–Walfisz theorem was obtained by Arnold Walfisz as an application of a theorem by Carl Ludwig Siegel to primes in arithmetic progressions. It is a refinement both of the prime number theorem and of Dirichlet's theorem on primes in arithmetic progressions.

In mathematics, the Chebyshev function is either of two related functions. The first Chebyshev functionϑ(x) or θ(x) is given by
In analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression.
In mathematics, the ATS theorem is the theorem on the approximation of a trigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful.
In graph theory, the Lovász number of a graph is a real number that is an upper bound on the Shannon capacity of the graph. It is also known as Lovász theta function and is commonly denoted by ϑ(G). This quantity was first introduced by László Lovász in his 1979 paper On the Shannon Capacity of a Graph.
In number theory, the prime omega functions and count the number of prime factors of a natural number Thereby counts each distinct prime factor, whereas the related function counts the total number of prime factors of honoring their multiplicity. For example, if we have a prime factorization of of the form for distinct primes , then the respective prime omega functions are given by and . These prime factor counting functions have many important number theoretic relations.
Christopher Hooley was a British mathematician, professor of mathematics at Cardiff University. He did his PhD under the supervision of Albert Ingham. He won the Adams Prize of Cambridge University in 1973. He was elected a Fellow of the Royal Society in 1983. He was also a Founding Fellow of the Learned Society of Wales.
Bruce Carl Berndt is an American mathematician. Berndt attended college at Albion College, graduating in 1961, where he also ran track. He received his master's and doctoral degrees from the University of Wisconsin–Madison. He lectured for a year at the University of Glasgow and then, in 1967, was appointed an assistant professor at the University of Illinois at Urbana-Champaign, where he has remained since. In 1973–74 he was a visiting scholar at the Institute for Advanced Study in Princeton. He is currently Michio Suzuki Distinguished Research Professor of Mathematics at the University of Illinois.
Nigel Boston is a British-American mathematician, who has made notable contributions to algebraic number theory, group theory, and arithmetic geometry.