
A Fourier series is a sum that represents a periodic function as a sum of sine and cosine waves. The frequency of each wave in the sum, or harmonic, is an integer multiple of the periodic function's fundamental frequency. Each harmonic's phase and amplitude can be determined using harmonic analysis. A Fourier series may potentially contain an infinite number of harmonics. Summing part of but not all the harmonics in a function's Fourier series produces an approximation to that function. For example, using the first few harmonics of the Fourier series for a square wave yields an approximation of a square wave.

Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern, and pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:

In mathematics, Stirling's approximation is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of . It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x).

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives. It is named after Francesco Faà di Bruno, although he was not the first to state or prove the formula. In 1800, more than 50 years before Faà di Bruno, the French mathematician Louis François Antoine Arbogast had stated the formula in a calculus textbook, which is considered to be the first published reference on the subject.
In game theory, a cooperative game is a game with competition between groups of players ("coalitions") due to the possibility of external enforcement of cooperative behavior. Those are opposed to non-cooperative games in which there is either no possibility to forge alliances or all agreements need to be self-enforcing.
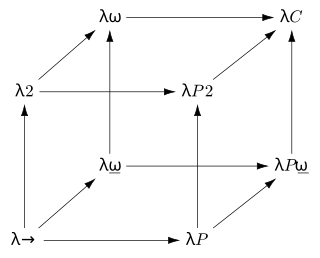
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:
The Stackelberg leadership model is a strategic game in economics in which the leader firm moves first and then the follower firms move sequentially. It is named after the German economist Heinrich Freiherr von Stackelberg who published Market Structure and Equilibrium in 1934, which described the model. In game theory terms, the players of this game are a leader and a follower and they compete on quantity. The Stackelberg leader is sometimes referred to as the Market Leader.

In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In electromagnetics, directivity is a parameter of an antenna or optical system which measures the degree to which the radiation emitted is concentrated in a single direction. It is the ratio of the radiation intensity in a given direction from the antenna to the radiation intensity averaged over all directions. Therefore, the directivity of a hypothetical isotropic radiator is 1, or 0 dBi.

Approximations for the mathematical constant pi in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era. In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century.

In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted simply as and .
Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.
Tail value at risk (TVaR), also known as tail conditional expectation (TCE) or conditional tail expectation (CTE), is a risk measure associated with the more general value at risk. It quantifies the expected value of the loss given that an event outside a given probability level has occurred.

In mathematics, the argument of a complex number z, denoted arg(z), is the angle between the positive real axis and the line joining the origin and z, represented as a point in the complex plane, shown as in Figure 1. It is a multi-valued function operating on the nonzero complex numbers. To define a single-valued function, the principal value of the argument is used. It is often chosen to be the unique value of the argument that lies within the interval (−π, π].
Cooperative bargaining is a process in which two people decide how to share a surplus that they can jointly generate. In many cases, the surplus created by the two players can be shared in many ways, forcing the players to negotiate which division of payoffs to choose. Such surplus-sharing problems are faced by management and labor in the division of a firm's profit, by trade partners in the specification of the terms of trade, and more.
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I, a seventh-century Indian mathematician. This formula is given in his treatise titled Mahabhaskariya. It is not known how Bhaskara I arrived at his approximation formula. However, several historians of mathematics have put forward different hypotheses as to the method Bhaskara might have used to arrive at his formula. The formula is elegant, simple and enables one to compute reasonably accurate values of trigonometric sines without using any geometry whatsoever.
In oligopoly theory, conjectural variation is the belief that one firm has an idea about the way its competitors may react if it varies its output or price. The firm forms a conjecture about the variation in the other firm's output that will accompany any change in its own output. For example, in the classic Cournot model of oligopoly, it is assumed that each firm treats the output of the other firms as given when it chooses its output. This is sometimes called the "Nash conjecture" as it underlies the standard Nash equilibrium concept. However, alternative assumptions can be made. Suppose you have two firms producing the same good, so that the industry price is determined by the combined output of the two firms. Now suppose that each firm has what is called the "Bertrand Conjecture" of −1. This means that if firm A increases its output, it conjectures that firm B will reduce its output to exactly offset firm A's increase, so that total output and hence price remains unchanged. With the Bertrand Conjecture, the firms act as if they believe that the market price is unaffected by their own output, because each firm believes that the other firm will adjust its output so that total output will be constant. At the other extreme is the Joint-Profit maximizing conjecture of +1. In this case each firm believes that the other will imitate exactly any change in output it makes, which leads to the firms behaving like a single monopoly supplier.
























