Barycentric

Last updated March 13, 2019

Barycentric can refer to:

In astronomy,

Barycentric coordinates (astronomy), coordinates defined by the common center of mass of two or more bodies
Barycentric Dynamical Time, a former time standard in the Solar system
Barycentric Coordinate Time, a coordinate time standard in the Solar system
Barycentre, the point between two objects where they balance each other

Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar System. TDB is now defined as a linear scaling of Barycentric Coordinate Time (TCB). A feature that distinguishes TDB from TCB is that TDB, when observed from the Earth's surface, has a difference from Terrestrial Time (TT) that is about as small as can be practically arranged with consistent definition: the differences are mainly periodic, and overall will remain at less than 2 milliseconds for several millennia.

Barycentric Coordinate Time is a coordinate time standard intended to be used as the independent variable of time for all calculations pertaining to orbits of planets, asteroids, comets, and interplanetary spacecraft in the Solar system. It is equivalent to the proper time experienced by a clock at rest in a coordinate frame co-moving with the barycenter of the Solar system: that is, a clock that performs exactly the same movements as the Solar system but is outside the system's gravity well. It is therefore not influenced by the gravitational time dilation caused by the Sun and the rest of the system.

In geometry,

Barycentric subdivision, a way of dividing a simplicial complex
Barycentric coordinates (mathematics), coordinates defined by the vertices of a simplex

In geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.

In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.

Simplex generalization of the notion of a triangle or tetrahedron to arbitrary dimensions

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. Specifically, a k-simplex is a k-dimensional polytope which is the convex hull of its k + 1 vertices. More formally, suppose the k + 1 points $are affinely independent, which means are linearly independent. Then, the simplex determined by them is the set of points$

This disambiguation page lists articles associated with the title Barycentric.
If an internal link led you here, you may wish to change the link to point directly to the intended article.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Related Research Articles

A time standard is a specification for measuring time: either the rate at which time passes; or points in time; or both. In modern times, several time specifications have been officially recognized as standards, where formerly they were matters of custom and practice. An example of a kind of time standard can be a time scale, specifying a method for measuring divisions of time. A standard for civil time can specify both time intervals and time-of-day.

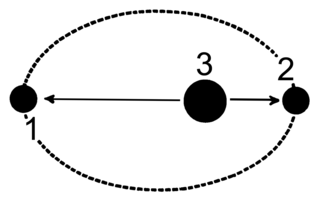
The term apsis refers to an extreme point in the orbit of an object. It denotes either the points on the orbit, or the respective distance of the bodies. The word comes via Latin from Greek, there denoting a whole orbit, and is cognate with apse. Except for the theoretical possibility of one common circular orbit for two bodies of equal mass at diametral positions, there are two apsides for any elliptic orbit, named with the prefixes peri- and ap-/apo- added to a reference to the body being orbited. All periodic orbits are, according to Newton's Laws of motion, ellipses: either the two individual ellipses of both bodies, with the center of mass of this two-body system at the one common focus of the ellipses, or the orbital ellipses, with one body taken as fixed at one focus, and the other body orbiting this focus. All these ellipses share a straight line, the line of apsides, that contains their major axes, the foci, and the vertices, and thus also the periapsis and the apoapsis. The major axis of the orbital ellipse is the distance of the apsides, when taken as points on the orbit, or their sum, when taken as distances.

In astronomy, the barycenter is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. It is an important concept in such fields as astronomy and astrophysics. The distance from a body's center of mass to the barycenter can be calculated as a two-body problem.

Geocentric Coordinate Time is a coordinate time standard intended to be used as the independent variable of time for all calculations pertaining to precession, nutation, the Moon, and artificial satellites of the Earth. It is equivalent to the proper time experienced by a clock at rest in a coordinate frame co-moving with the center of the Earth: that is, a clock that performs exactly the same movements as the Earth but is outside the Earth's gravity well. It is therefore not influenced by the gravitational time dilation caused by the Earth.

The astronomical system of units, formally called the IAU (1976) System of Astronomical Constants, is a system of measurement developed for use in astronomy. It was adopted by the International Astronomical Union (IAU) in 1976, and has been significantly updated in 1994 and 2009.

Comet Machholz, formally designated C/2004 Q2, is a long-period comet discovered by Donald Machholz on August 27, 2004. It reached naked eye brightness in January 2005. Unusual for such a relatively bright comet, its perihelion was farther from the Sun than the Earth's orbit.

In the theory of relativity, it is convenient to express results in terms of a spacetime coordinate system relative to an implied observer. In many coordinate systems, an event is specified by one time coordinate and three spatial coordinates. The time specified by the time coordinate is referred to as coordinate time to distinguish it from proper time.

The Eclipse Comet of 1948, formally known as C/1948 V1, was an especially bright comet discovered during a solar eclipse on November 1, 1948. Although there have been several comets that have been seen during solar eclipses, the Eclipse Comet of 1948 is perhaps the best-known; it was however, best viewed only from the Southern Hemisphere.

C/2001 Q4 (NEAT) is a comet with an unusual, almost perpendicular retrograde orbit which brings it into the inner solar system by a deeply southward path. It initially emerged from its remote home spending most of its time near the south celestial pole. This comet was discovered on August 24, 2001 by the Near-Earth Asteroid Tracking program (NEAT).

Comet Zhu–Balam is a long-period comet first identified by David D. Balam on June 8, 1997 and originally photographed by Gin Zhu on June 3, 1997. The comet is estimated at 10 kilometres in diameter with a period of approximately 36,800 years.

C/1992 J1 is a comet that was discovered 1 May 1992 by David Rabinowitz of the Spacewatch Project. This was the first comet to be discovered using an automated system.

C/2000 W1 (Utsunomiya-Jones) is a long-period comet discovered on November 18, 2000, by Syogo Utsunomiya and Albert F. A. L. Jones.

C/1999 F1 (Catalina) is one of the longest known long-period comets. It was discovered on March 23, 1999, by the Catalina Sky Survey.

C/2000 U5 (LINEAR) is a single-apparition comet discovered on October 29, 2000, by Lincoln Near-Earth Asteroid Research. The comet has an observation arc of 362 days allowing a good estimate of the orbit. C/2000 U5 is, as of 2015, the 13th most hyperbolic comet ever discovered and will leave the Solar System.

The barycentric celestial reference system (BCRS) is a coordinate system used in astrometry to specify the location and motions of astronomical objects. It was created in 2000 by the International Astronomical Union (IAU) to be the global standard reference system for objects located outside the gravitational vicinity of Earth: planets, moons, and other Solar System bodies, stars and other objects in the Milky Way galaxy, and extra-galactic objects.

C/2012 S4 is a non-periodic comet with the largest listed aphelion of any object on the JPL Small-Body Database. But the listed aphelion distance of 500,000 AU (8 ly) from the Sun is a generic near-perihelion unperturbed two-body solution that assumes the Sun and comet are the only two objects in the Universe. Other comets, such as C/2015 TQ209 and C/2017 A3 (Elenin) have had epoch-dependent solutions with aphelia of more than 1,000,000 AU (16 ly). As a comparison, the closest star, Proxima Centauri, is about 4.24 light years from the Sun, and Wolf 359 is 7.78 light years away. Any comet more than about 150,000 AU (2 ly) from the Sun can be considered lost to the interstellar medium. Using an epoch when C/2012 S4 is beyond the planetary region of the Solar System, it is clear C/2012 S4 will not be ejected from the Solar System.

(418993) 2009 MS₉, provisionally known as 2009 MS₉, is a centaur roughly 30–60 km in diameter. It has a highly inclined orbit and a barycentric semi-major axis (average distance from the Sun) of ~353 AU.

2017 MB₇ is a trans-Neptunian object and damocloid on a cometary-like orbit from the outer Solar System, approximately 6 kilometers (4 miles) in diameter. It was first observed on 22 June 2017 by the Pan-STARRS survey at Haleakala Observatory in Hawaii, United States. The unusual object has the largest heliocentric aphelion of any known minor planet, even larger than that of 2014 FE72.