
In mathematics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.
In mathematics, the adele ring of a global field is a central object of class field theory, a branch of algebraic number theory. It is the restricted product of all the completions of the global field, and is an example of a self-dual topological ring.
In mathematics, the Plancherel theorem is a result in harmonic analysis, proven by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum. That is, if is a function on the real line, and is its frequency spectrum, then

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function.
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics. The Hamilton–Jacobi equation is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.
In mathematics, a real or complex-valued function f on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, α > 0, such that
In quantum field theory and statistical mechanics, the Mermin–Wagner theorem states that continuous symmetries cannot be spontaneously broken at finite temperature in systems with sufficiently short-range interactions in dimensions d ≤ 2. Intuitively, this means that long-range fluctuations can be created with little energy cost and since they increase the entropy they are favored.
In mathematics, the Riesz potential is a potential named after its discoverer, the Hungarian mathematician Marcel Riesz. In a sense, the Riesz potential defines an inverse for a power of the Laplace operator on Euclidean space. They generalize to several variables the Riemann–Liouville integrals of one variable.
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.
In mathematics, Gårding's inequality is a result that gives a lower bound for the bilinear form induced by a real linear elliptic partial differential operator. The inequality is named after Lars Gårding.
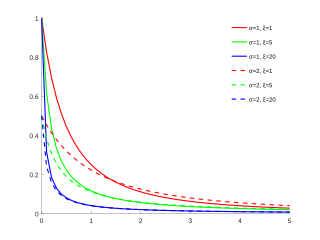
In statistics, the generalized Pareto distribution (GPD) is a family of continuous probability distributions. It is often used to model the tails of another distribution. It is specified by three parameters: location , scale , and shape . Sometimes it is specified by only scale and shape and sometimes only by its shape parameter. Some references give the shape parameter as .
In Riemannian geometry and pseudo-Riemannian geometry, the Gauss–Codazzi equations are fundamental formulas which link together the induced metric and second fundamental form of a submanifold of a Riemannian or pseudo-Riemannian manifold.
Bilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data. Such methods are used where one needs to deal with a situation where the frequency composition of a signal may be changing over time; this sub-field used to be called time–frequency signal analysis, and is now more often called time–frequency signal processing due to the progress in using these methods to a wide range of signal-processing problems.
In mathematics, the Besov space is a complete quasinormed space which is a Banach space when 1 ≤ p, q ≤ ∞. These spaces, as well as the similarly defined Triebel–Lizorkin spaces, serve to generalize more elementary function spaces such as Sobolev spaces and are effective at measuring regularity properties of functions.
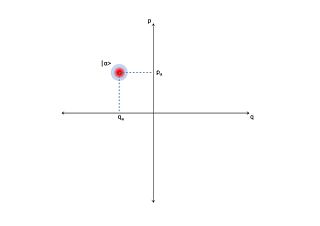
In quantum optics, an optical phase space is a phase space in which all quantum states of an optical system are described. Each point in the optical phase space corresponds to a unique state of an optical system. For any such system, a plot of the quadratures against each other, possibly as functions of time, is called a phase diagram. If the quadratures are functions of time then the optical phase diagram can show the evolution of a quantum optical system with time.
Uncertainty theory is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms.
In mathematics, the oscillator representation is a projective unitary representation of the symplectic group, first investigated by Irving Segal, David Shale, and André Weil. A natural extension of the representation leads to a semigroup of contraction operators, introduced as the oscillator semigroup by Roger Howe in 1988. The semigroup had previously been studied by other mathematicians and physicists, most notably Felix Berezin in the 1960s. The simplest example in one dimension is given by SU(1,1). It acts as Möbius transformations on the extended complex plane, leaving the unit circle invariant. In that case the oscillator representation is a unitary representation of a double cover of SU(1,1) and the oscillator semigroup corresponds to a representation by contraction operators of the semigroup in SL(2,C) corresponding to Möbius transformations that take the unit disk into itself.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems.








