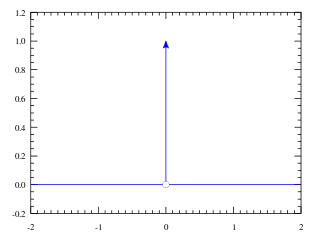
In mathematical analysis, the Dirac delta function, also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be represented heuristically as

In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the distribution of a normalized version of the sample mean converges to a standard normal distribution. This holds even if the original variables themselves are not normally distributed. There are several versions of the CLT, each applying in the context of different conditions.

In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence. They can be thought of in a similar fashion for a function. For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit.
In probability theory, there exist several different notions of convergence of sequences of random variables, including convergence in probability, convergence in distribution, and almost sure convergence. The different notions of convergence capture different properties about the sequence, with some notions of convergence being stronger than others. For example, convergence in distribution tells us about the limit distribution of a sequence of random variables. This is a weaker notion than convergence in probability, which tells us about the value a random variable will take, rather than just the distribution.

In probability theory, the law of large numbers (LLN) is a mathematical law that states that the average of the results obtained from a large number of independent random samples converges to the true value, if it exists. More formally, the LLN states that given a sample of independent and identically distributed values, the sample mean converges to the true mean.
In information theory, the asymptotic equipartition property (AEP) is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of data compression.
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function.
Vapnik–Chervonenkis theory was developed during 1960–1990 by Vladimir Vapnik and Alexey Chervonenkis. The theory is a form of computational learning theory, which attempts to explain the learning process from a statistical point of view.
In mathematics, the Radon–Nikodym theorem is a result in measure theory that expresses the relationship between two measures defined on the same measurable space. A measure is a set function that assigns a consistent magnitude to the measurable subsets of a measurable space. Examples of a measure include area and volume, where the subsets are sets of points; or the probability of an event, which is a subset of possible outcomes within a wider probability space.
In probability theory, a Chernoff bound is an exponentially decreasing upper bound on the tail of a random variable based on its moment generating function. The minimum of all such exponential bounds forms the Chernoff or Chernoff-Cramér bound, which may decay faster than exponential. It is especially useful for sums of independent random variables, such as sums of Bernoulli random variables.

In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter θ0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to θ0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to θ0 converges to one.
In mathematics, more specifically measure theory, there are various notions of the convergence of measures. For an intuitive general sense of what is meant by convergence of measures, consider a sequence of measures μn on a space, sharing a common collection of measurable sets. Such a sequence might represent an attempt to construct 'better and better' approximations to a desired measure μ that is difficult to obtain directly. The meaning of 'better and better' is subject to all the usual caveats for taking limits; for any error tolerance ε > 0 we require there be N sufficiently large for n ≥ N to ensure the 'difference' between μn and μ is smaller than ε. Various notions of convergence specify precisely what the word 'difference' should mean in that description; these notions are not equivalent to one another, and vary in strength.
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; in particular, every local martingale that is bounded from below is a supermartingale, and every local martingale that is bounded from above is a submartingale; however, a local martingale is not in general a martingale, because its expectation can be distorted by large values of small probability. In particular, a driftless diffusion process is a local martingale, but not necessarily a martingale.
Convergence in measure is either of two distinct mathematical concepts both of which generalize the concept of convergence in probability.
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales.
In real analysis and measure theory, the Vitali convergence theorem, named after the Italian mathematician Giuseppe Vitali, is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is a characterization of the convergence in Lp in terms of convergence in measure and a condition related to uniform integrability.
In probability theory, the continuous mapping theorem states that continuous functions preserve limits even if their arguments are sequences of random variables. A continuous function, in Heine's definition, is such a function that maps convergent sequences into convergent sequences: if xn → x then g(xn) → g(x). The continuous mapping theorem states that this will also be true if we replace the deterministic sequence {xn} with a sequence of random variables {Xn}, and replace the standard notion of convergence of real numbers “→” with one of the types of convergence of random variables.
The exponential mechanism is a technique for designing differentially private algorithms. It was developed by Frank McSherry and Kunal Talwar in 2007. Their work was recognized as a co-winner of the 2009 PET Award for Outstanding Research in Privacy Enhancing Technologies.
This article is supplemental for “Convergence of random variables” and provides proofs for selected results.





















