
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single force. Thus, if the temperature is high enough – approximately 1015 K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 1015 K has not been seen widely throughout the universe since before the quark epoch, and currently the highest human-made temperature in thermal equilibrium is around 5.5×1012 K (from the Large Hadron Collider).
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.

In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.
In physics and engineering, a constitutive equation or constitutive relation is a relation between two or more physical quantities that is specific to a material or substance or field, and approximates its response to external stimuli, usually as applied fields or forces. They are combined with other equations governing physical laws to solve physical problems; for example in fluid mechanics the flow of a fluid in a pipe, in solid state physics the response of a crystal to an electric field, or in structural analysis, the connection between applied stresses or loads to strains or deformations.
A Hopfield network is a form of recurrent neural network, or a spin glass system, that can serve as a content-addressable memory. The Hopfield network, named for John Hopfield, consists of a single layer of neurons, where each neuron is connected to every other neuron except itself. These connections are bidirectional and symmetric, meaning the weight of the connection from neuron i to neuron j is the same as the weight from neuron j to neuron i. Patterns are associatively recalled by fixing certain inputs, and dynamically evolve the network to minimize an energy function, towards local energy minimum states that correspond to stored patterns. Patterns are associatively learned by a Hebbian learning algorithm.

The Wheeler–DeWitt equation for theoretical physics and applied mathematics, is a field equation attributed to John Archibald Wheeler and Bryce DeWitt. The equation attempts to mathematically combine the ideas of quantum mechanics and general relativity, a step towards a theory of quantum gravity.
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.
In physics, precisely in the study of the theory of general relativity and many alternatives to it, the post-Newtonian formalism is a calculational tool that expresses Einstein's (nonlinear) equations of gravity in terms of the lowest-order deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields, it may be preferable to solve the complete equations numerically. Some of these post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of the matter forming the gravitational field to the speed of light, which in this case is better called the speed of gravity. In the limit, when the fundamental speed of gravity becomes infinite, the post-Newtonian expansion reduces to Newton's law of gravity.
In theoretical physics, the Wess–Zumino model has become the first known example of an interacting four-dimensional quantum field theory with linearly realised supersymmetry. In 1974, Julius Wess and Bruno Zumino studied, using modern terminology, dynamics of a single chiral superfield whose cubic superpotential leads to a renormalizable theory. It is a special case of 4D N = 1 global supersymmetry.

In physics, canonical quantum gravity is an attempt to quantize the canonical formulation of general relativity. It is a Hamiltonian formulation of Einstein's general theory of relativity. The basic theory was outlined by Bryce DeWitt in a seminal 1967 paper, and based on earlier work by Peter G. Bergmann using the so-called canonical quantization techniques for constrained Hamiltonian systems invented by Paul Dirac. Dirac's approach allows the quantization of systems that include gauge symmetries using Hamiltonian techniques in a fixed gauge choice. Newer approaches based in part on the work of DeWitt and Dirac include the Hartle–Hawking state, Regge calculus, the Wheeler–DeWitt equation and loop quantum gravity.

In biochemistry, metabolic control analysis (MCA) is a mathematical framework for describing metabolic, signaling, and genetic pathways. MCA quantifies how variables, such as fluxes and species concentrations, depend on network parameters. In particular, it is able to describe how network-dependent properties, called control coefficients, depend on local properties called elasticities or elasticity coefficients.

The Gaussian network model (GNM) is a representation of a biological macromolecule as an elastic mass-and-spring network to study, understand, and characterize the mechanical aspects of its long-time large-scale dynamics. The model has a wide range of applications from small proteins such as enzymes composed of a single domain, to large macromolecular assemblies such as a ribosome or a viral capsid. Protein domain dynamics plays key roles in a multitude of molecular recognition and cell signalling processes. Protein domains, connected by intrinsically disordered flexible linker domains, induce long-range allostery via protein domain dynamics. The resultant dynamic modes cannot be generally predicted from static structures of either the entire protein or individual domains.
In chemistry, the rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant, the concentration of products, and other effectors. The degree to which these factors change the reaction rate is described by the elasticity coefficient. This coefficient is defined as follows:

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.

Stefan Schuster is a German biophysicist. He is professor for bioinformatics at the University of Jena.
Bimetric gravity or bigravity refers to two different classes of theories. The first class of theories relies on modified mathematical theories of gravity in which two metric tensors are used instead of one. The second metric may be introduced at high energies, with the implication that the speed of light could be energy-dependent, enabling models with a variable speed of light.

Eberhard O. Voit is a Clinical Professor at the University of Texas at Dallas. Until 2024, he was a Professor and David D. Flanagan Chair in Biological Systems at the Georgia Institute of Technology, where is now Professor Emeritus, and a Georgia Research Alliance Eminent Scholar. He leads the Laboratory for Biological Systems Analysis.
In biochemistry, a rate-limiting step is a reaction step that controls the rate of a series of biochemical reactions. The statement is, however, a misunderstanding of how a sequence of enzyme-catalyzed reaction steps operate. Rather than a single step controlling the rate, it has been discovered that multiple steps control the rate. Moreover, each controlling step controls the rate to varying degrees.
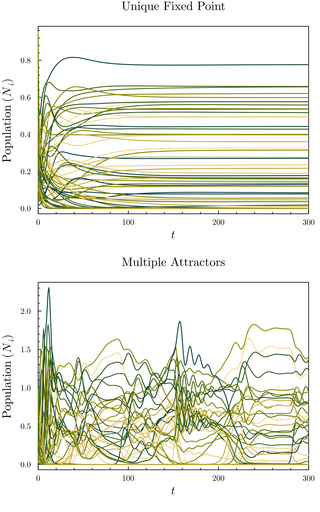
The random generalized Lotka–Volterra model (rGLV) is an ecological model and random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to competition from the presence of other species. It is often analyzed in the many-species limit using tools from statistical physics, in particular from spin glass theory.
In supersymmetry, 4D supergravity is the theory of supergravity in four dimensions with a single supercharge. It contains exactly one supergravity multiplet, consisting of a graviton and a gravitino, but can also have an arbitrary number of chiral and vector supermultiplets, with supersymmetry imposing stringent constraints on how these can interact. The theory is primarily determined by three functions, those being the Kähler potential, the superpotential, and the gauge kinetic matrix. Many of its properties are strongly linked to the geometry associated to the scalar fields in the chiral multiplets. After the simplest form of this supergravity was first discovered, a theory involving only the supergravity multiplet, the following years saw an effort to incorporate different matter multiplets, with the general action being derived in 1982 by Eugène Cremmer, Sergio Ferrara, Luciano Girardello, and Antonie Van Proeyen.












