Black Path Game

Last updated January 28, 2025

The Black Path Game (also known by various other names, such as Brick) is a two-player board game described and analysed in Winning Ways for your Mathematical Plays . It was invented by Larry Black in 1960.^[1]

It has also been reported that a game known as "Black" or "Black's Game" was invented in 1960 by William L. Black. This "William L. Black" (possibly known as "Larry") was at that time an undergraduate at the Massachusetts Institute of Technology, investigating Hex and Bridg-It , two games based on the challenge to create a connected "chain" of counters that link opposite sides of a game board. The creative outcome of Black's research was a new topological game that his friends (perhaps unimaginatively) called Black. The game was introduced to the public by Martin Gardner in his October 1963 "Mathematical Games column" in Scientific American .^[2]

Rules

The Black Path Game is played on a board ruled into squares. One edge on the boundary of the board is designated to be the start of the path. After the first move, the players extend the path away from the starting edge by alternately filling the adjacent square at the end of the current path with one of three configurations shown below.

Any square that is not empty is filled with one of the following configurations that contains two paths linking two sides:

T1 tile, with paths connecting adjacent sides (top and left, and bottom and right)
T2 tile, with paths connecting adjacent sides (top and right, and bottom and left)
T3 tile, with paths connecting opposite sides (top and bottom, and left and right)

These tiles are the three ways to join the sides of the square in pairs. The first two are the tiles of the Truchet tiling.^[3]

The path may return to a previously filled square and follow the yet-unused segment on that square. The player who first causes the path to run back into the edge of the board loses the game.^[1]

Strategy

As outlined in the example games provided, the player who routes the path into a corner of the board will win the game, as the other player will have no choice but to run the path into the edge of the board.^[2]

For a rectangular board with an even number of squares, the first player has a winning strategy. This occurs when at least one side-length is even. Imagine the board covered with rectangular (2×1 unit-size) dominoes. If the first player always plays so the end of the path falls on the middle of one of the dominoes, that player will win. This strategy was discovered by Black's friend Elwyn R. Berlekamp,^[2] who subsequently described it in his book.^[1]

4×4 board (16 cells total)
	A	B	C	D
1					1
2					2
3					3
4					4
	A	B	C	D

5×5 board (25 cells total)
	A	B	C	D	E
1						1
2						2
3						3
4						4
5						5
	A	B	C	D	E

For a rectangular board with an odd total number of squares, i.e., when both sides of the board are odd, the second player can instead win by using a similar domino tiling strategy occupying every square except the one containing the first player's first move.^[1]

Logic

The domino tiling strategy works by making the losing player end the path on the edge of a new domino; by continuing the path on the new domino, the winning player will eventually force the losing player to the edge or a corner.^[2]

The second player can win on a board with an even number of square cells; first consider the board completely covered with 2×1 dominoes except for the upper left and lower right corners. If Player 2 forces Player 1 to move in [B2], the second cell of the main diagonal, regardless of Player 1's move in [B2], the unused path in [B2] will connect two squares which can be regarded as the two squares of a "split domino" that Player 2 can use, and the remaining tiles (save the lower-right corner) can be covered in dominoes.^[2]

Refer to the three examples below, illustrating the "split domino" that results from the third move:

[A1]-T3
[A2]-T2

3: [B2]-T1, path to [B1]
	A	B	C	D
1					1
2			S		2
3		S			3
4					4
	A	B	C	D

3: [B2]-T2, path to [B3]
	A	B	C	D
1		S			1
2			S		2
3					3
4					4
	A	B	C	D

3: [B2]-T3, path to [C2]
	A	B	C	D
1		S			1
2					2
3		S			3
4					4
	A	B	C	D

Examples

	A	B	C	D
1					1
2					2
3					3
4					4
	A	B	C	D

Consider the example game shown at right on a 4×4 grid, where the moves have been:

[A1]-T2
[B1]-T2
[B2]-T3
[B3]-T2
[C3]-T1
[C2]-T2
[A2]-T1
[A3]-T2

According to the rules, the next move by Player 1 (odd-numbered turns) must be in space [B4] to continue the path. If Player 1 makes the move [B4]-T3 that will result in an instant loss, since this tile will link the path to the bottom edge. Playing [B4]-T1 will result in a win, as Player 2's following move is placed in the corner [A4] and Player 3 will lose regardless of the piece played. Playing [B4]-T2 results in an eventual loss for Player 1;^[1] comparison to the 4×4 domino-tiled blank board shows that Player 1 making the move [B4]-T1 puts the path into the middle of the domino, while [B4]-T2 puts the path onto the edge of the domino, and Player 2 can maneuver Player 1 into making the last move.

	A	B	C	D
1					1
2					2
3					3
4					4
	A	B	C	D

Gardner describes a second example game, where the moves have been:

[A1]-T3
[A2]-T2
[B2]-T3
[C2]-T1
[C1]-T2
[B1]-T1
[B3]-T2
[C3]-T1
[D2]-T1

In this second example, Player 1 has maneuvered the path into the corner space [D1], which results in a win regardless of the move made by Player 2.^[2] After the third move (by Player 2) in [B2]-T3, the split domino exists in cells [B1] and [B3]. However, the fifth move by Player 2 [C1]-T2 brought the path to the edge of the split domino, which Player 1 took advantage of with the sixth move [B1]-T1, playing to the middle of the split domino.

Related Research Articles

<span class="mw-page-title-main">Dominoes</span> Family of tile-based games

Dominoes is a family of tile-based games played with gaming pieces. Each domino is a rectangular tile, usually with a line dividing its face into two square ends. Each end is marked with a number of spots or is blank. The backs of the tiles in a set are indistinguishable, either blank or having some common design. The gaming pieces make up a domino set, sometimes called a deck or pack. The traditional European domino set consists of 28 tiles, also known as pieces, bones, rocks, stones, men, cards or just dominoes, featuring all combinations of spot counts between zero and six. A domino set is a generic gaming device, similar to playing cards or dice, in that a variety of games can be played with a set. Another form of entertainment using domino pieces is the practice of domino toppling.

In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric. In other words, the only difference between player 1 and player 2 is that player 1 goes first. The game is played until a terminal position is reached. A terminal position is one from which no moves are possible. Then one of the players is declared the winner and the other the loser. Furthermore, impartial games are played with perfect information and no chance moves, meaning all information about the game and operations for both players are visible to both players.

Patrol chess is a chess variant in which captures can be made and checks given only if the capturing or checking piece is guarded by a friendly unit. Non-capturing and non-checking moves are played as normal.

<span class="mw-page-title-main">Rubik's Magic</span> Mechanical puzzle created by Erno Rubik

Rubik's Magic, like the Rubik's Cube, is a mechanical puzzle invented by Ernő Rubik and first manufactured by Matchbox in the mid-1980s.

GIPF is an abstract strategy board game by Kris Burm, the first of seven games in his series of games called the GIPF Project. GIPF was recommended by Spiel des Jahres in 1998.

<span class="mw-page-title-main">Trax (game)</span> Strategy game

Trax is a two-player abstract strategy game of loops and lines invented by David Smith in 1980.

In mathematics, the axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person topological games of length ω. AD states that every game of a certain type is determined; that is, one of the two players has a winning strategy.

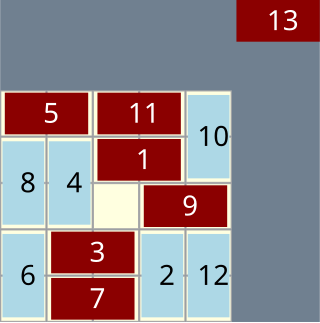
<span class="mw-page-title-main">Domineering</span> Mathematical game

Domineering is a mathematical game that can be played on any collection of squares on a sheet of graph paper. For example, it can be played on a 6×6 square, a rectangle, an entirely irregular polyomino, or a combination of any number of such components. Two players have a collection of dominoes which they place on the grid in turn, covering up squares. One player places tiles vertically, while the other places them horizontally. As in most games in combinatorial game theory, the first player who cannot move loses.

Tsuro is a tile-based board game designed by Tom McMurchie, originally published by WizKids and now published by Calliope Games.

Muggins, sometimes also called All Fives, is a domino game played with any of the commonly available sets. Although suitable for up to four players, Muggins is described by John McLeod as "a good, quick two player game".

The mutilated chessboard problem is a tiling puzzle posed by Max Black in 1946 that asks:

Suppose a standard 8×8 chessboard has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2×1 so as to cover all of these squares?

In geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominoes, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.

<i>Backtrackin</i> 1984 compilation album by Eric Clapton

Backtrackin' is a two-disc compilation album by Eric Clapton spanning the years 1966 to 1980. It was released in 1984. The compilation contains all of Clapton's best known songs with Cream, Blind Faith, Derek and the Dominos, and his solo 1970s work through his 1980 live album Just One Night. This compilation album is made in Germany and is only available in the United States as an import. It was originally released by Starblend Records, and has since been reissued by Polydor Records. This 2 CD compilation is currently out of print in some markets while still available in some form in others.

In mathematics, a domino is a polyomino of order 2, that is, a polygon in the plane made of two equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there is only one free domino.

Onyx is a two-player abstract strategy board game invented by Larry Back in 1995. The game features a rule for performing captures, making Onyx unique among connection games.

Dameo is an abstract strategy board game for two players invented by Christian Freeling in 2000. It is a variant of the game draughts and is played on an 8×8 checkered gameboard.

In information visualization and graphic design, Truchet tiles are square tiles decorated with patterns that are not rotationally symmetric. When placed in a square tiling of the plane, they can form varied patterns, and the orientation of each tile can be used to visualize information associated with the tile's position within the tiling.

<span class="mw-page-title-main">Glossary of domino terms</span>

The following is a glossary of terms used in dominoes. Besides the terms listed here, there are numerous regional or local slang terms. Terms in this glossary should not be game-specific, i.e. specific to one particular version of dominoes, but apply to a wide range of domino games. For glossaries that relate primarily to one game or family of similar games, see the relevant article.

Le Trioker is a corner-matching puzzle game played using 25 equilateral triangle-shaped tiles. Each corner is marked with zero, one, two, or three dots and newly placed pieces must match the values on pieces already placed on the game board, similar to the gameplay of the earlier Triominoes.

References

1 2 3 4 5 Berlekamp, Elwyn R.; Conway, John H.; Guy, Richard K. (1982), "The Black Path Game", Winning Ways for your Mathematical Plays, Vol. 2: Games in Particular, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], pp. 682–683, MR 0654502 .
1 2 3 4 5 6 Gardner, Martin (1983). "5: Four Unusual Board Games". Sixth Book of Mathematical Diversions from 'Scientific American' . Chicago: University of Chicago Press. pp. 39–47. ISBN 0226282503.
↑ Browne, Cameron (2008), "Truchet curves and surfaces", Computers & Graphics, 32 (2): 268–281, doi:10.1016/j.cag.2007.10.001, Truchet-style tiles are used as the basis for several strategy games including Trax, Meander and the Black Path Game, all of which predate Smith's seminal 1987 article that associates such tiles with the work of Sébastien Truchet.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[ww-1] 1 2 3 4 5 Berlekamp, Elwyn R.; Conway, John H.; Guy, Richard K. (1982), "The Black Path Game", Winning Ways for your Mathematical Plays, Vol. 2: Games in Particular, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], pp. 682–683, MR 0654502 .

[Gardner-2] 1 2 3 4 5 6 Gardner, Martin (1983). "5: Four Unusual Board Games". Sixth Book of Mathematical Diversions from 'Scientific American' . Chicago: University of Chicago Press. pp. 39–47. ISBN 0226282503.

[3] Browne, Cameron (2008), "Truchet curves and surfaces", Computers & Graphics, 32 (2): 268–281, doi:10.1016/j.cag.2007.10.001, Truchet-style tiles are used as the basis for several strategy games including Trax, Meander and the Black Path Game, all of which predate Smith's seminal 1987 article that associates such tiles with the work of Sébastien Truchet.

[1]

[2]

[3]