Related Research Articles

A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised machine learning technique used to produce a low-dimensional representation of a higher dimensional data set while preserving the topological structure of the data. For example, a data set with p variables measured in n observations could be represented as clusters of observations with similar values for the variables. These clusters then could be visualized as a two-dimensional "map" such that observations in proximal clusters have more similar values than observations in distal clusters. This can make high-dimensional data easier to visualize and analyze.
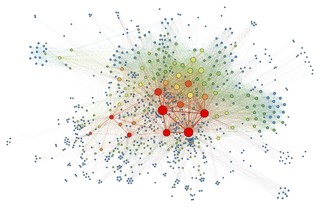
Force-directed graph drawing algorithms are a class of algorithms for drawing graphs in an aesthetically-pleasing way. Their purpose is to position the nodes of a graph in two-dimensional or three-dimensional space so that all the edges are of more or less equal length and there are as few crossing edges as possible, by assigning forces among the set of edges and the set of nodes, based on their relative positions, and then using these forces either to simulate the motion of the edges and nodes or to minimize their energy.
In graph theory, a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties; this likelihood tends to be greater than the average probability of a tie randomly established between two nodes.

In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.

In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to.
In mathematics, a graph partition is the reduction of a graph to a smaller graph by partitioning its set of nodes into mutually exclusive groups. Edges of the original graph that cross between the groups will produce edges in the partitioned graph. If the number of resulting edges is small compared to the original graph, then the partitioned graph may be better suited for analysis and problem-solving than the original. Finding a partition that simplifies graph analysis is a hard problem, but one that has applications to scientific computing, VLSI circuit design, and task scheduling in multiprocessor computers, among others. Recently, the graph partition problem has gained importance due to its application for clustering and detection of cliques in social, pathological and biological networks. For a survey on recent trends in computational methods and applications see Buluc et al. (2013). Two common examples of graph partitioning are minimum cut and maximum cut problems.

A computer cluster is a set of computers that work together so that they can be viewed as a single system. Unlike grid computers, computer clusters have each node set to perform the same task, controlled and scheduled by software.
Split-brain is a computer term, based on an analogy with the medical Split-brain syndrome. It indicates data or availability inconsistencies originating from the maintenance of two separate data sets with overlap in scope, either because of servers in a network design, or a failure condition based on servers not communicating and synchronizing their data to each other. This last case is also commonly referred to as a network partition.
Anuška Ferligoj is a Slovenian mathematician, born August 19, 1947 in Ljubljana, Slovenia, whose specialty is network analysis. Her specific interests include multivariate analysis, social networks, and survey methodology. She is Fellow of the European Academy of Sociology.

Exponential family random graph models (ERGMs) are a family of statistical models for analyzing data from social and other networks. Examples of networks examined using ERGM include knowledge networks, organizational networks, colleague networks, social media networks, networks of scientific development, and others.
In graph theory and network analysis, node influence metrics are measures that rank or quantify the influence of every node within a graph. They are related to centrality indices. Applications include measuring the influence of each person in a social network, understanding the role of infrastructure nodes in transportation networks, the Internet, or urban networks, and the participation of a given node in disease dynamics.

Blockmodeling is a set or a coherent framework, that is used for analyzing social structure and also for setting procedure(s) for partitioning (clustering) social network's units, based on specific patterns, which form a distinctive structure through interconnectivity. It is primarily used in statistics, machine learning and network science.
Aleš Žiberna is a Slovene statistician, whose specialty is network analysis. His specific research interests include blockmodeling, multivariate analysis and computer intensive methods.
Blockmodel in blockmodeling is defined as a multitude of structures, which are obtained with:
In generalized blockmodeling, the blockmodeling is done by "the translation of an equivalence type into a set of permitted block types", which differs from the conventional blockmodeling, which is using the indirect approach. It's a special instance of the direct blockmodeling approach.
Patrick Doreian is a American mathematician and social scientist, whose specialty is network analysis. His specific research interests include blockmodeling, social structure and network processeses.
Deterministic blockmodeling is approach in blockmodeling, that does not assume probabilistic model, and instead relies on the exact or approximate algorithms, which are used to find blockmodel(s). This approach minimizes some inconsistency, that can accure with the ideal block structure. Such approach can be used only for analysis of nominal valued networks.
Generalized blockmodeling of valued networks is an approach of the generalized blockmodeling, dealing with valued networks.
Homogeneity blockmodeling is an approach in blockmodeling, which is best suited for a preliminary or main approach to valued networks, when a prior knowledge about these networks is not available. This is due to the fact, that homogeneity blockmodeling emphasizes the similarity of link (tie) strengths within the blocks over the pattern of links. In this approach, tie (link) values are assumed to be equal (homogenous) within blocks.
Linked network in statistics is a network, which is composed of one-node networks, where the nodes from different one-node networks are connected through two-node networks. This means, that "linked networks are collections of networks defined on different sets of nodes", where all sets of nodes must be connected to each other.
References
- 1 2 3 Žiberna, Aleš (2018). "Chapter 10: Blockmodeling linked networks". In Doreian, Patrick; Batagelj, Vladimir; Ferligoj, Anuška (eds.). Advances in Network Clustering and Blockmodeling. John Wiley & Sons, Inc. pp. 259–280.
- 1 2 Žiberna, Aleš (2014). "Blockmodeling of multilevel networks". Social Networks. 39: 46–61. doi:10.1016/j.socnet.2014.04.002.
- ↑ Žiberna, Aleš (2020). "k-means-based algorithm for blockmodeling linked networks". Social Networks. 61: 153–169. doi:10.1016/j.socnet.2019.10.006.