In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants . The determinant of a matrix A is denoted det(A), det A, or |A|.
In linear algebra, the Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.

In group theory, the quaternion group Q8 (sometimes just denoted by Q) is a non-abelian group of order eight, isomorphic to the eight-element subset of the quaternions under multiplication. It is given by the group presentation

In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation.

In mathematics, the name symplectic group can refer to two different, but closely related, collections of mathematical groups, denoted Sp(2n, F) and Sp(n) for positive integer n and field F. The latter is called the compact symplectic group and is also denoted by . Many authors prefer slightly different notations, usually differing by factors of 2. The notation used here is consistent with the size of the most common matrices which represent the groups. In Cartan's classification of the simple Lie algebras, the Lie algebra of the complex group Sp(2n, C) is denoted Cn, and Sp(n) is the compact real form of Sp(2n, C). Note that when we refer to the (compact) symplectic group it is implied that we are talking about the collection of (compact) symplectic groups, indexed by their dimension n.
In linear algebra, an n-by-n square matrix A is called invertible, if there exists an n-by-n square matrix B such that
In mathematics, and in particular linear algebra, the Moore–Penrose inverse of a matrix is the most widely known generalization of the inverse matrix. It was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951, and Roger Penrose in 1955. Earlier, Erik Ivar Fredholm had introduced the concept of a pseudoinverse of integral operators in 1903. When referring to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose inverse. The term generalized inverse is sometimes used as a synonym for pseudoinverse.
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).
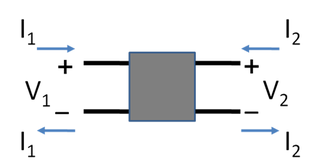
A two-port network is an electrical network (circuit) or device with two pairs of terminals to connect to external circuits. Two terminals constitute a port if the currents applied to them satisfy the essential requirement known as the port condition: the electric current entering one terminal must equal the current emerging from the other terminal on the same port. The ports constitute interfaces where the network connects to other networks, the points where signals are applied or outputs are taken. In a two-port network, often port 1 is considered the input port and port 2 is considered the output port.
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.
Scattering parameters or S-parameters describe the electrical behavior of linear electrical networks when undergoing various steady state stimuli by electrical signals.
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4.
In mathematical physics, the gamma matrices, , also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra Cl1,3(). It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin-1/2 particles.
In physics, the Majorana equation is a relativistic wave equation. It is named after the Italian physicist Ettore Majorana, who proposed it in 1937 as a means of describing fermions that are their own antiparticle. Particles corresponding to this equation are termed Majorana particles, although that term now has a more expansive meaning, referring to any fermionic particle that is its own anti-particle.
The following are important identities involving derivatives and integrals in vector calculus.
In signal processing, a polyphase matrix is a matrix whose elements are filter masks. It represents a filter bank as it is used in sub-band coders alias discrete wavelet transforms.
The Eckart conditions, named after Carl Eckart, simplify the nuclear motion (rovibrational) Hamiltonian that arises in the second step of the Born–Oppenheimer approximation. They make it possible to approximately separate rotation from vibration. Although the rotational and vibrational motions of the nuclei in a molecule cannot be fully separated, the Eckart conditions minimize the coupling close to a reference configuration. The Eckart conditions are explained by Louck and Galbraith and in Section 10.2 of the textbook by Bunker and Jensen, where a numerical example is given.
In mathematics, specifically multilinear algebra, a dyadic or dyadic tensor is a second order tensor, written in a notation that fits in with vector algebra.
In the mathematical discipline of numerical linear algebra, a matrix splitting is an expression which represents a given matrix as a sum or difference of matrices. Many iterative methods depend upon the direct solution of matrix equations involving matrices more general than tridiagonal matrices. These matrix equations can often be solved directly and efficiently when written as a matrix splitting. The technique was devised by Richard S. Varga in 1960.
In mathematics, the Frobenius inner product is a binary operation that takes two matrices and returns a scalar. It is often denoted . The operation is a component-wise inner product of two matrices as though they are vectors, and satisfies the axioms for an inner product. The two matrices must have the same dimension - same number of rows and columns, but are not restricted to be square matrices.



















