 | Look up Boolean algebra in Wiktionary, the free dictionary. |
Boolean algebra is the algebra of truth values and operations on them.
Boolean algebra may also refer to:
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.
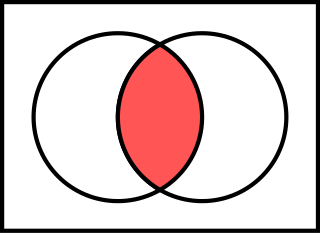
In logic, mathematics and linguistics, And is the truth-functional operator of logical conjunction; the and of a set of operands is true if and only if all of its operands are true. The logical connective that represents this operator is typically written as or ⋅ .
In mathematics, a Boolean ringR is a ring for which x2 = x for all x in R, that is, a ring that consists only of idempotent elements. An example is the ring of integers modulo 2.
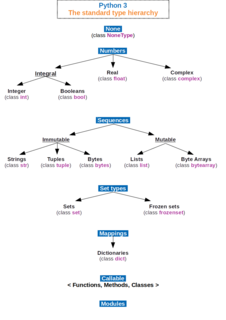
In computer science and computer programming, a data type or simply type is an attribute of data which tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers, floating-point numbers, characters and Booleans. A data type constrains the values that an expression, such as a variable or a function, might take. This data type defines the operations that can be done on the data, the meaning of the data, and the way values of that type can be stored. A data type provides a set of values from which an expression may take its values.
In mathematics, an algebraic structure consists of a nonempty set A, a collection of operations on A of finite arity, and a finite set of identities, known as axioms, that these operations must satisfy.
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.
Term may refer to:
Any kind of logic, function, expression, or theory based on the work of George Boole is considered Boolean.
In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy. LoF describes three distinct logical systems:
Topological Boolean algebra may refer to:
The word 'algebra' is used for various branches and structures of mathematics. For their overview, see Algebra.
In mathematics and abstract algebra, the two-element Boolean algebra is the Boolean algebra whose underlying setB is the Boolean domain. The elements of the Boolean domain are 1 and 0 by convention, so that B = {0, 1}. Paul Halmos's name for this algebra "2" has some following in the literature, and will be employed here.
In mathematics, a free Boolean algebra is a Boolean algebra with a distinguished set of elements, called generators, such that:
1+1 is a mathematical expression that evaluates to:
In mathematics, there are many types of algebraic structures which are studied. Abstract algebra is primarily the study of specific algebraic structures and their properties. Algebraic structures may be viewed in different ways, however the common starting point of algebra texts is that an algebraic object incorporates one or more sets with one or more binary operations or unary operations satisfying a collection of axioms.
Boolean algebra is a mathematically rich branch of abstract algebra. Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under zero or more operations satisfying certain equations.
In mathematical logic, algebraic logic is the reasoning obtained by manipulating equations with free variables.
Algebra is one of the broad areas of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. It includes everything from elementary equation solving to the study of abstractions such as groups, rings, and fields. The more basic parts of algebra are called elementary algebra; the more abstract parts are called abstract algebra or modern algebra. Elementary algebra is generally considered to be essential for any study of mathematics, science, or engineering, as well as such applications as medicine and economics. Abstract algebra is a major area in advanced mathematics, studied primarily by professional mathematicians.
In mathematics and mathematical logic, Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0, respectively. Instead of elementary algebra, where the values of the variables are numbers and the prime operations are addition and multiplication, the main operations of Boolean algebra are the conjunction (and) denoted as ∧, the disjunction (or) denoted as ∨, and the negation (not) denoted as ¬. It is thus a formalism for describing logical operations, in the same way that elementary algebra describes numerical operations.