Boolean ring

Last updated

In mathematics, a Boolean ringR is a ring for which x2 = x for all x in R, that is, a ring that consists of only idempotent elements. [1] [2] [3] An example is the ring of integers modulo 2.

Contents

Every Boolean ring gives rise to a Boolean algebra, with ring multiplication corresponding to conjunction or meet ∧, and ring addition to exclusive disjunction or symmetric difference (not disjunction ∨, [4] which would constitute a semiring). Conversely, every Boolean algebra gives rise to a Boolean ring. Boolean rings are named after the founder of Boolean algebra, George Boole.

Notation

There are at least four different and incompatible systems of notation for Boolean rings and algebras:

Historically, the term "Boolean ring" has been used to mean a "Boolean ring possibly without an identity", and "Boolean algebra" has been used to mean a Boolean ring with an identity. The existence of the identity is necessary to consider the ring as an algebra over the field of two elements: otherwise there cannot be a (unital) ring homomorphism of the field of two elements into the Boolean ring. (This is the same as the old use of the terms "ring" and "algebra" in measure theory. [lower-alpha 1] )

Examples

One example of a Boolean ring is the power set of any set X, where the addition in the ring is symmetric difference, and the multiplication is intersection. As another example, we can also consider the set of all finite or cofinite subsets of X, again with symmetric difference and intersection as operations. More generally with these operations any field of sets is a Boolean ring. By Stone's representation theorem every Boolean ring is isomorphic to a field of sets (treated as a ring with these operations).

Relation to Boolean algebras

Venn diagrams for the Boolean operations of conjunction, disjunction, and complement Vennandornot.svg
Venn diagrams for the Boolean operations of conjunction, disjunction, and complement

Since the join operation ∨ in a Boolean algebra is often written additively, it makes sense in this context to denote ring addition by ⊕, a symbol that is often used to denote exclusive or.

Given a Boolean ring R, for x and y in R we can define

x ∧ y = xy,
x ∨ y = x ⊕ y ⊕ xy,
¬x = 1 ⊕ x.

These operations then satisfy all of the axioms for meets, joins, and complements in a Boolean algebra. Thus every Boolean ring becomes a Boolean algebra. Similarly, every Boolean algebra becomes a Boolean ring thus:

xy = x ∧ y,
x ⊕ y = (x ∨ y) ∧ ¬(x ∧ y).

If a Boolean ring is translated into a Boolean algebra in this way, and then the Boolean algebra is translated into a ring, the result is the original ring. The analogous result holds beginning with a Boolean algebra.

A map between two Boolean rings is a ring homomorphism if and only if it is a homomorphism of the corresponding Boolean algebras. Furthermore, a subset of a Boolean ring is a ring ideal (prime ring ideal, maximal ring ideal) if and only if it is an order ideal (prime order ideal, maximal order ideal) of the Boolean algebra. The quotient ring of a Boolean ring modulo a ring ideal corresponds to the factor algebra of the corresponding Boolean algebra modulo the corresponding order ideal.

Properties of Boolean rings

Every Boolean ring R satisfies x ⊕ x = 0 for all x in R, because we know

x ⊕ x = (x ⊕ x)2 = x2 ⊕ x2 ⊕ x2 ⊕ x2 = x ⊕ x ⊕ x ⊕ x

and since (R, ⊕) is an abelian group, we can subtract x ⊕ x from both sides of this equation, which gives x ⊕ x = 0. A similar proof shows that every Boolean ring is commutative:

x ⊕ y = (x ⊕ y)2 = x2 ⊕ xy ⊕ yx ⊕ y2 = x ⊕ xy ⊕ yx ⊕ y and this yields xy ⊕ yx = 0, which means xy = yx (using the first property above).

The property x ⊕ x = 0 shows that any Boolean ring is an associative algebra over the field F2 with two elements, in precisely one way.[ citation needed ] In particular, any finite Boolean ring has as cardinality a power of two. Not every unital associative algebra over F2 is a Boolean ring: consider for instance the polynomial ring F2[X].

The quotient ring R / I of any Boolean ring R modulo any ideal I is again a Boolean ring. Likewise, any subring of a Boolean ring is a Boolean ring.

Any localization RS−1 of a Boolean ring R by a set S ⊆ R is a Boolean ring, since every element in the localization is idempotent.

The maximal ring of quotients Q(R) (in the sense of Utumi and Lambek) of a Boolean ring R is a Boolean ring, since every partial endomorphism is idempotent. [6]

Every prime ideal P in a Boolean ring R is maximal: the quotient ring R / P is an integral domain and also a Boolean ring, so it is isomorphic to the field F2, which shows the maximality of P. Since maximal ideals are always prime, prime ideals and maximal ideals coincide in Boolean rings.

Every finitely generated ideal of a Boolean ring is principal (indeed, (x,y) = (x + y + xy)). Furthermore, as all elements are idempotents, Boolean rings are commutative von Neumann regular rings and hence absolutely flat, which means that every module over them is flat.

Unification

Unification in Boolean rings is decidable, [7] that is, algorithms exist to solve arbitrary equations over Boolean rings. Both unification and matching in finitely generated free Boolean rings are NP-complete, and both are NP-hard in finitely presented Boolean rings. [8] (In fact, as any unification problem f(X) = g(X) in a Boolean ring can be rewritten as the matching problem f(X) + g(X) = 0, the problems are equivalent.)

Unification in Boolean rings is unitary if all the uninterpreted function symbols are nullary and finitary otherwise (i.e. if the function symbols not occurring in the signature of Boolean rings are all constants then there exists a most general unifier, and otherwise the minimal complete set of unifiers is finite). [9]

See also

Notes

  1. ↑ When a Boolean ring has an identity, then a complement operation becomes definable on it, and a key characteristic of the modern definitions of both Boolean algebra and sigma-algebra is that they have complement operations.

Citations

  1. ↑ Fraleigh 1976, pp. 25, 200
  2. ↑ Herstein 1975, pp. 130, 268
  3. ↑ McCoy 1968, p. 46
  4. ↑ "Disjunction as sum operation in Boolean Ring".
  5. ↑ Koppelberg 1989, Definition 1.1, p. 7
  6. ↑ Brainerd & Lambek 1959, Corollary 2
  7. ↑ Martin & Nipkow 1986
  8. ↑ Kandri-Rody, Kapur & Narendran 1985
  9. ↑ Boudet, Jouannaud & Schmidt-Schauß 1989

Related Research Articles

<span class="mw-page-title-main">Associative algebra</span> Ring that is also a vector space or a module

In mathematics, an associative algebraA over a commutative ring K is a ring A together with a ring homomorphism from K into the center of A. This is thus an algebraic structure with an addition, a multiplication, and a scalar multiplication. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a module or vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over K. A standard first example of a K-algebra is a ring of square matrices over a commutative ring K, with the usual matrix multiplication.

<span class="mw-page-title-main">Boolean algebra (structure)</span> Algebraic structure modeling logical operations

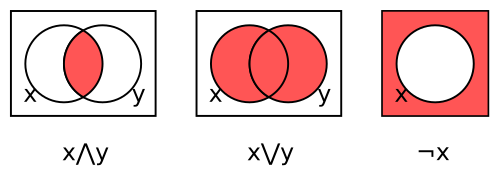
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.

<span class="mw-page-title-main">Integral domain</span> Commutative ring with no zero divisors other than zero

In mathematics, an integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibility. In an integral domain, every nonzero element a has the cancellation property, that is, if a ≠ 0, an equality ab = ac implies b = c.

<span class="mw-page-title-main">Product of rings</span> Ring built from other rings (mathematics)

In mathematics, a product of rings or direct product of rings is a ring that is formed by the Cartesian product of the underlying sets of several rings, equipped with componentwise operations. It is a direct product in the category of rings.

<span class="mw-page-title-main">Ideal (ring theory)</span> Additive subgroup of a mathematical ring that absorbs multiplication

In mathematics, and more specifically in ring theory, an ideal of a ring is a special subset of its elements. Ideals generalize certain subsets of the integers, such as the even numbers or the multiples of 3. Addition and subtraction of even numbers preserves evenness, and multiplying an even number by any integer results in an even number; these closure and absorption properties are the defining properties of an ideal. An ideal can be used to construct a quotient ring in a way similar to how, in group theory, a normal subgroup can be used to construct a quotient group.

<span class="mw-page-title-main">Semigroup</span> Algebraic structure consisting of a set with an associative binary operation

In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it.

In mathematics, more specifically in ring theory, a maximal ideal is an ideal that is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if there are no other ideals contained between I and R.

<span class="mw-page-title-main">Ring (mathematics)</span> Algebraic structure with addition and multiplication

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. Informally, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.

In mathematics, more specifically ring theory, the Jacobson radical of a ring R is the ideal consisting of those elements in R that annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same ideal, and so the notion is left-right symmetric. The Jacobson radical of a ring is frequently denoted by J(R) or rad(R); the former notation will be preferred in this article, because it avoids confusion with other radicals of a ring. The Jacobson radical is named after Nathan Jacobson, who was the first to study it for arbitrary rings in Jacobson 1945.

<span class="mw-page-title-main">Quotient ring</span> Reduction of a ring by one of its ideals

In ring theory, a branch of abstract algebra, a quotient ring, also known as factor ring, difference ring or residue class ring, is a construction quite similar to the quotient group in group theory and to the quotient space in linear algebra. It is a specific example of a quotient, as viewed from the general setting of universal algebra. Starting with a ring R and a two-sided ideal I in R, a new ring, the quotient ring R / I, is constructed, whose elements are the cosets of I in R subject to special + and ⋅ operations.

Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.

In algebra, a unit or invertible element of a ring is an invertible element for the multiplication of the ring. That is, an element u of a ring R is a unit if there exists v in R such that

In ring theory, a branch of mathematics, an idempotent element or simply idempotent of a ring is an element a such that a2 = a. That is, the element is idempotent under the ring's multiplication. Inductively then, one can also conclude that a = a2 = a3 = a4 = ... = an for any positive integer n. For example, an idempotent element of a matrix ring is precisely an idempotent matrix.

In mathematics, particularly in algebra, the class of projective modules enlarges the class of free modules over a ring, by keeping some of the main properties of free modules. Various equivalent characterizations of these modules appear below.

In ring theory, a branch of mathematics, a ring is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0. A commutative algebra over a commutative ring is called a reduced algebra if its underlying ring is reduced.

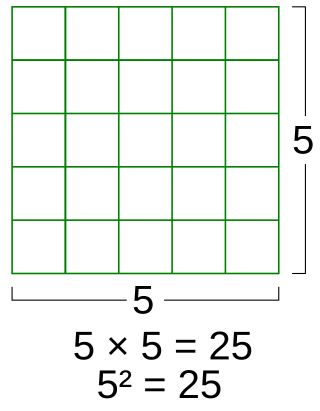
<span class="mw-page-title-main">Square (algebra)</span> Product of a number by itself

In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.

Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.

GF(2) is the finite field with two elements. Notations Z2 and may be encountered although they can be confused with the notation of 2-adic integers.

In ring theory, a branch of mathematics, a ring R is a polynomial identity ring if there is, for some N > 0, an element P ≠ 0 of the free algebra, Z⟨X1, X2, ..., XN⟩, over the ring of integers in N variables X1, X2, ..., XN such that

This is a glossary of commutative algebra.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.