In graph theory, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes.

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges.
In graph theory, two graphs and are homeomorphic if there is a graph isomorphism from some subdivision of to some subdivision of . If the edges of a graph are thought of as lines drawn from one vertex to another, then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if they are homeomorphic in the topological sense.

In mathematics, Sperner's lemma is a combinatorial result on colorings of triangulations, analogous to the Brouwer fixed point theorem, which is equivalent to it. It states that every Sperner coloring of a triangulation of an -dimensional simplex contains a cell whose vertices all have different colors.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).
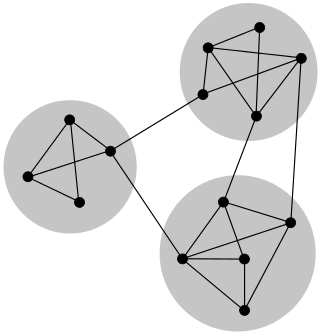
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

In mathematics, and more specifically in graph theory, a multigraph is a graph which is permitted to have multiple edges, that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge.
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition. These edges are said to cross the cut. In a connected graph, each cut-set determines a unique cut, and in some cases cuts are identified with their cut-sets rather than with their vertex partitions.
In mathematics, a biased graph is a graph with a list of distinguished circles, such that if two circles in the list are contained in a theta graph, then the third circle of the theta graph is also in the list. A biased graph is a generalization of the combinatorial essentials of a gain graph and in particular of a signed graph.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees equals twice the number of edges in the graph. Both results were proven by Leonhard Euler in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.
In graph theory, a Trémaux tree of an undirected graph is a type of spanning tree, generalizing depth-first search trees. They are defined by the property that every edge of connects an ancestor–descendant pair in the tree. Trémaux trees are named after Charles Pierre Trémaux, a 19th-century French author who used a form of depth-first search as a strategy for solving mazes. They have also been called normal spanning trees, especially in the context of infinite graphs.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte, states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

In graph theory, the Gallai–Edmonds decomposition is a partition of the vertices of a graph into three subsets which provides information on the structure of maximum matchings in the graph. Tibor Gallai and Jack Edmonds independently discovered it and proved its key properties.








