Related Research Articles

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure whose internal nodes each store a key greater than all the keys in the node’s left subtree and less than those in its right subtree. A binary tree is a type of data structure for storing data such as numbers in an organized way. Binary search trees allow binary search for fast lookup, addition and removal of data items, and can be used to implement dynamic sets and lookup tables. The order of nodes in a BST means that each comparison skips about half of the remaining tree, so the whole lookup takes time proportional to the binary logarithm of the number of items stored in the tree. This is much better than the linear time required to find items by key in an (unsorted) array, but slower than the corresponding operations on hash tables. Several variants of the binary search tree have been studied.
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as disks. It is commonly used in databases and file systems.

In computer science, a data structure is a data organization, management, and storage format that enables efficient access and modification. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data, i.e., it is an algebraic structure about data.

In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
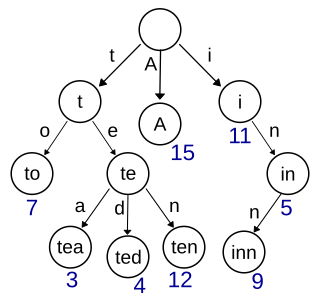
In computer science, a trie, also called digital tree or prefix tree, is a type of search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.
In computer science, an associative array, map, symbol table, or dictionary is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection. Not to be confused with Associative Processors
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.

In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key and creating point clouds. k-d trees are a special case of binary space partitioning trees.
A database index is a data structure that improves the speed of data retrieval operations on a database table at the cost of additional writes and storage space to maintain the index data structure. Indexes are used to quickly locate data without having to search every row in a database table every time a database table is accessed. Indexes can be created using one or more columns of a database table, providing the basis for both rapid random lookups and efficient access of ordered records.

In computing, data is any sequence of one or more symbols. Datum is a single symbol of data. Data requires interpretation to become information. Digital data is data that is represented using the binary number system of ones (1) and zeros (0), as opposed to analog representation. In modern (post-1960) computer systems, all data is digital.
A database model is a type of data model that determines the logical structure of a database. It fundamentally determines in which manner data can be stored, organized and manipulated. The most popular example of a database model is the relational model, which uses a table-based format.
Database tables and indexes may be stored on disk in one of a number of forms, including ordered/unordered flat files, ISAM, heap files, hash buckets, or B+ trees. Each form has its own particular advantages and disadvantages. The most commonly used forms are B-trees and ISAM. Such forms or structures are one aspect of the overall schema used by a database engine to store information.

In computer science, a Cartesian tree is a binary tree derived from a sequence of numbers; it can be uniquely defined from the properties that it is heap-ordered and that a symmetric (in-order) traversal of the tree returns the original sequence. Introduced by Vuillemin (1980) in the context of geometric range searching data structures, Cartesian trees have also been used in the definition of the treap and randomized binary search tree data structures for binary search problems. The Cartesian tree for a sequence may be constructed in linear time using a stack-based algorithm for finding all nearest smaller values in a sequence.
A sorted array is an array data structure in which each element is sorted in numerical, alphabetical, or some other order, and placed at equally spaced addresses in computer memory. It is typically used in computer science to implement static lookup tables to hold multiple values which have the same data type. Sorting an array is useful in organising data in ordered form and recovering them rapidly.
In phylogenetics, a single-access key is an identification key where the sequence and structure of identification steps is fixed by the author of the key. At each point in the decision process, multiple alternatives are offered, each leading to a result or a further choice. The alternatives are commonly called "leads", and the set of leads at a given point a "couplet".
In computer science, integer sorting is the algorithmic problem of sorting a collection of data values by integer keys. Algorithms designed for integer sorting may also often be applied to sorting problems in which the keys are floating point numbers, rational numbers, or text strings. The ability to perform integer arithmetic on the keys allows integer sorting algorithms to be faster than comparison sorting algorithms in many cases, depending on the details of which operations are allowed in the model of computing and how large the integers to be sorted are.
In computer science, a fractal tree index is a tree data structure that keeps data sorted and allows searches and sequential access in the same time as a B-tree but with insertions and deletions that are asymptotically faster than a B-tree. Like a B-tree, a fractal tree index is a generalization of a binary search tree in that a node can have more than two children. Furthermore, unlike a B-tree, a fractal tree index has buffers at each node, which allow insertions, deletions and other changes to be stored in intermediate locations. The goal of the buffers is to schedule disk writes so that each write performs a large amount of useful work, thereby avoiding the worst-case performance of B-trees, in which each disk write may change a small amount of data on disk. Like a B-tree, fractal tree indexes are optimized for systems that read and write large blocks of data. The fractal tree index has been commercialized in databases by Tokutek. Originally, it was implemented as a cache-oblivious lookahead array, but the current implementation is an extension of the Bε tree. The Bε is related to the Buffered Repository Tree. The Buffered Repository Tree has degree 2, whereas the Bε tree has degree Bε. The fractal tree index has also been used in a prototype filesystem. An open source implementation of the fractal tree index is available, which demonstrates the implementation details outlined below.
In computer science, a weak heap is a data structure for priority queues, combining features of the binary heap and binomial heap. It can be stored in an array as an implicit binary tree like a binary heap, and has the efficiency guarantees of binomial heaps.
References
- 1 2 Winston, J. 1999. Describing Species. Columbia University Press.
- ↑ The Natural History Museum 2000. Sorting creepy-crawlies. http://www.nhm.ac.uk/education/activities/school-activities/discovery-guides/assets/sorting.pdf