Related Research Articles

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

The Rubik's Cube is a 3-D combination puzzle originally invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube, the puzzle was licensed by Rubik to be sold by Pentangle Puzzles in the UK in 1978, and then by Ideal Toy Corp in 1980 via businessman Tibor Laczi and Seven Towns founder Tom Kremer. The cube was released internationally in 1980 and became one of the most recognized icons in popular culture. It won the 1980 German Game of the Year special award for Best Puzzle. As of January 2009, 350 million cubes had been sold worldwide, making it the world's bestselling puzzle game and bestselling toy. The Rubik's Cube was inducted into the US National Toy Hall of Fame in 2014.

In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .

In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number of integers along one side (n), and the constant sum is called the 'magic constant'. If the array includes just the positive integers , the magic square is said to be 'normal'. Some authors take magic square to mean normal magic square.
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube". A cuboid is like a cube in the sense that by adjusting the lengths of the edges or the angles between faces a cuboid can be transformed into a cube. In mathematical language a cuboid is a convex polyhedron whose polyhedral graph is the same as that of a cube.

In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.
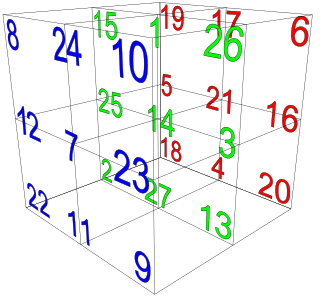
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a collection of integers arranged in an n × n × n pattern such that the sums of the numbers on each row, on each column, on each pillar and on each of the four main space diagonals are equal, the so-called magic constant of the cube, denoted M3(n). It can be shown that if a magic cube consists of the numbers 1, 2, ..., n3, then it has magic constant (sequence A027441 in the OEIS)
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars, and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant.
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares and magic cubes, that is, an n × n × n × ... × n array of integers such that the sums of the numbers on each pillar (along any axis) as well as on the main space diagonals are all the same. The common sum is called the magic constant of the hypercube, and is sometimes denoted Mk(n). If a magic hypercube consists of the numbers 1, 2, ..., nk, then it has magic number

In geometry, a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face as each other.
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.
In recreational mathematics, a pandiagonal magic cube is a magic cube with the additional property that all broken diagonals have the same sum as each other. Pandiagonal magic cubes are extensions of diagonal magic cubes and generalize pandiagonal magic squares to three dimensions.

A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.

The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an oblate tetrahedrille or shortened to obtetrahedrille.

In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.

The Sonobe module is one of the many units used to build modular origami. The popularity of Sonobe modular origami models derives from the simplicity of folding the modules, the sturdy and easy assembly, and the flexibility of the system.

A simple magic cube is the lowest of six basic classes of magic cubes. These classes are based on extra features required.
References
- ↑ Narins, Brigham (2001), World of mathematics, Volume 2, Gale Group, p. 391, ISBN 9780787650650 .
- ↑ Pickover, Clifford A. (2003), The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across Dimensions, Princeton University Press, p. 178, ISBN 1400841518 .