Calculus of predispositions is a basic part of predispositioning theory and belongs to the indeterministic procedures.
Calculus of predispositions is a basic part of predispositioning theory and belongs to the indeterministic procedures.
"The key component of any indeterministic procedure is the evaluation of a position. Since it is impossible to devise a deterministic chain linking the inter-mediate state with the outcome of the game, the most complex component of any indeterministic method is assessing these intermediate stages. It is precisely the function of predispositions to assess the impact of an intermediate state upon the future course of development." [1]
According to Aron Katsenelinboigen, calculus of predispositions is another method of computing probability. Both methods may lead to the same results and, thus, can be interchangeable. However, it is not always possible to interchange them since computing via frequencies requires availability of statistics, possibility to gather the data as well as having the knowledge of the extent to which one can interlink the system’s constituent elements. Also, no statistics can be obtained on unique events and, naturally, in such cases the calculus of predispositions becomes the only option.
The procedure of calculating predispositions is linked to two steps – dissection of the system on its constituent elements and integration of the analyzed parts in a new whole. According to Katsenelinboigen, the system is structured by two basic types of parameters – material and positional. The material parameters constitute the skeleton of the system. Relationships between them form positional parameters. The calculus of predispositions primarily deals with
"In order to quantify the evaluation of a position we need new techniques, which I have grouped under the heading of calculus of predispositions. This calculus is based on a weight function, which represents a variation on the well-known criterion of optimality for local extremum.
This criterion incorporates material parameters and their conditional valuations.
The following key elements distinguish the modified weight function from the criterion of optimality:
There are some differences between frequency-based and predispositions-based methods of computing probability.
The procedure of calculating predispositions is linked to two steps – dissection of the system on its constituent elements and integration of the analyzed parts in a new whole.
According to Katsenelinboigen, the two methods of computing probability may complement each other if, for instance, they are applied to a multilevel system with an increasing complexity of its composition at higher levels.
A parameter, generally, is any characteristic that can help in defining or classifying a particular system. That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc.

Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.

Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".
Nonparametric statistics is a type of statistical analysis that does not rely on the assumption of a specific underlying distribution, or any other specific assumptions about the population parameters. This is in contrast to parametric statistics, which make such assumptions about the population. In nonparametric statistics, a distribution may not be specified at all, or a distribution may be specified but its parameters, such as the mean and variance, are not assumed to have a known value or distribution in advance. In some cases, parameters may be generated from the data, such as the median. Nonparametric statistics can be used for descriptive statistics or statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are evidently violated.
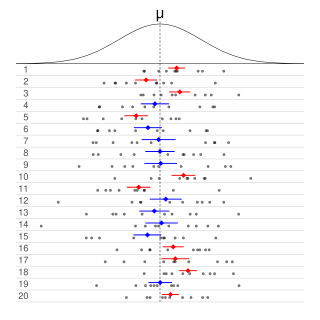
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated confidence level; the 95% confidence level is most common, but other levels, such as 90% or 99%, are sometimes used. The confidence level, degree of confidence or confidence coefficient represents the long-run proportion of CIs that theoretically contain the true value of the parameter; this is tantamount to the nominal coverage probability. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value.
Indeterminism is the idea that events are not caused, or are not caused deterministically.

Libertarianism is one of the main philosophical positions related to the problems of free will and determinism which are part of the larger domain of metaphysics. In particular, libertarianism is an incompatibilist position which argues that free will is logically incompatible with a deterministic universe. Libertarianism states that since agents have free will, determinism must be false and vice versa.

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory.

In the design of experiments, optimal experimental designs are a class of experimental designs that are optimal with respect to some statistical criterion. The creation of this field of statistics has been credited to Danish statistician Kirstine Smith.
Many letters of the Latin alphabet, both capital and small, are used in mathematics, science, and engineering to denote by convention specific or abstracted constants, variables of a certain type, units, multipliers, or physical entities. Certain letters, when combined with special formatting, take on special meaning.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.
Predispositioning theory, in the field of decision theory and systems theory, is a theory focusing on the stages between a complete order and a complete disorder.

Aron Iosifovich Katsenelinboigen was a founder of predispositioning theory, a subject in decision theory and systems theory that models development in the context of uncertainty.
Approximate Bayesian computation (ABC) constitutes a class of computational methods rooted in Bayesian statistics that can be used to estimate the posterior distributions of model parameters.
Frequentist inference is a type of statistical inference based in frequentist probability, which treats “probability” in equivalent terms to “frequency” and draws conclusions from sample-data by means of emphasizing the frequency or proportion of findings in the data. Frequentist-inference underlies frequentist statistics, in which the well-established methodologies of statistical hypothesis testing and confidence intervals are founded.
The principle of the impossibility of a gambling system is a concept in probability. It states that in a random sequence, the methodical selection of subsequences does not change the probability of specific elements. The first mathematical demonstration is attributed to Richard von Mises.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.