Related Research Articles

Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a tornado in Brazil.

Ferromagnetism is a property of certain materials that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagnetic materials are familiar metals that are noticeably attracted to a magnet, a consequence of their substantial magnetic permeability. Magnetic permeability describes the induced magnetization of a material due to the presence of an external magnetic field. This temporarily induced magnetization, for example, inside a steel plate, accounts for its attraction to the permanent magnet. Whether or not that steel plate acquires a permanent magnetization itself depends not only on the strength of the applied field but on the so-called coercivity of the ferromagnetic material, which can vary greatly.

Hysteresis is the dependence of the state of a system on its history. For example, a magnet may have more than one possible magnetic moment in a given magnetic field, depending on how the field changed in the past. Plots of a single component of the moment often form a loop or hysteresis curve, where there are different values of one variable depending on the direction of change of another variable. This history dependence is the basis of memory in a hard disk drive and the remanence that retains a record of the Earth's magnetic field magnitude in the past. Hysteresis occurs in ferromagnetic and ferroelectric materials, as well as in the deformation of rubber bands and shape-memory alloys and many other natural phenomena. In natural systems it is often associated with irreversible thermodynamic change such as phase transitions and with internal friction; and dissipation is a common side effect.

In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933.
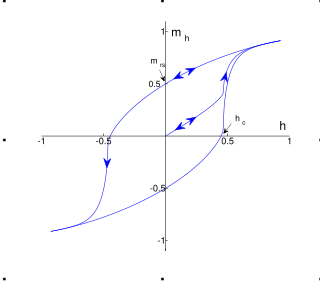
Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.

Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.

Giant magnetoresistance (GMR) is a quantum mechanical magnetoresistance effect observed in multilayers composed of alternating ferromagnetic and non-magnetic conductive layers. The 2007 Nobel Prize in Physics was awarded to Albert Fert and Peter Grünberg for the discovery of GMR.
Exchange bias or exchange anisotropy occurs in bilayers of magnetic materials where the hard magnetization behavior of an antiferromagnetic thin film causes a shift in the soft magnetization curve of a ferromagnetic film. The exchange bias phenomenon is of tremendous utility in magnetic recording, where it is used to pin the state of the readback heads of hard disk drives at exactly their point of maximum sensitivity; hence the term "bias."

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, namely that several different initial chaotic conditions evolve in phase space in a way that never repeats, so all chaos is unpredictable. This underscores that chaotic systems can be completely deterministic and yet still be inherently unpredictable over long periods of time. Because chaos continually increases in systems, we cannot predict the future of systems well. E.g., even the small flap of a butterfly’s wings could set the world on a vastly different trajectory, such as by causing a hurricane. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.
Complexity economics is the application of complexity science to the problems of economics. It relaxes several common assumptions in economics, including general equilibrium theory. While it does not reject the existence of an equilibrium, it sees such equilibria as "a special case of nonequilibrium", and as an emergent property resulting from complex interactions between economic agents. The complexity science approach has also been applied to computational economics.
Reservoir computing is a framework for computation derived from recurrent neural network theory that maps input signals into higher dimensional computational spaces through the dynamics of a fixed, non-linear system called a reservoir. After the input signal is fed into the reservoir, which is treated as a "black box," a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The first key benefit of this framework is that training is performed only at the readout stage, as the reservoir dynamics are fixed. The second is that the computational power of naturally available systems, both classical and quantum mechanical, can be used to reduce the effective computational cost.
Originally, the Preisach model of hysteresis generalized magnetic hysteresis as the relationship between the magnetic field and magnetization of a magnetic material as the parallel connection of independent relay hysterons. It was first suggested in 1935 by Ferenc (Franz) Preisach in the German academic journal Zeitschrift für Physik. In the field of ferromagnetism, the Preisach model is sometimes thought to describe a ferromagnetic material as a network of small independently acting domains, each magnetized to a value of either or . A sample of iron, for example, may have evenly distributed magnetic domains, resulting in a net magnetic moment of zero.
John Barkley Rosser Jr. was a mathematical economist and Professor of Economics at James Madison University in Harrisonburg, Virginia since 1988. He was known for work in nonlinear economic dynamics, including applications in economics of catastrophe theory, chaos theory, and complexity theory. With Marina V. Rosser he invented the concept of the "new traditional economy". He introduced into economic discourse the concepts of chaotic bubbles, chaotic hysteresis, and econochemistry. He also invented the concepts of the megacorpstate and hypercyclic morphogenesis. He was the first to provide a mathematical model of the period of financial distress in a speculative bubble. With Marina V. Rosser and Ehsan Ahmed, he was the first to argue for a two-way positive link between income inequality and the size of an underground economy in a nation. Rosser's equation has been used to forecast ratios of future Social Security benefits to current ones in real terms.
Hypercyclic morphogenesis refers to the emergence of a higher order of self-reproducing structure or organization or hierarchy within a system, first introduced by J. Barkley Rosser, Jr. in 1991. It involves combining the idea of the hypercycle, an idea due to Manfred Eigen and Peter Schuster (1979) with that of morphogenesis, an idea due to D’Arcy W.Thompson (1917). The hypercycle involves the problem in biochemistry of molecules combining in a self-reacting group that is able to stay together, posited by Eigen and Schuster as the foundation for the emergence of multi-cellular organisms. Thompson saw morphogenesis as a central part of the development of an organism as cell differentiation led to new organs appearing as it develops and grows. Alan Turing (1952) would study the chemistry and mathematics involved in such a process, which would also be studied mathematically by René Thom (1972) in his formulation of catastrophe theory.
A coupled map lattice (CML) is a dynamical system that models the behavior of non-linear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases.
In structural engineering, the Bouc–Wen model of hysteresis is one of the most used hysteretic models typically employed to describe non-linear hysteretic systems. It was introduced by Robert Bouc and extended by Yi-Kwei Wen, who demonstrated its versatility by producing a variety of hysteretic patterns. This model is able to capture, in analytical form, a range of hysteretic cycle shapes matching the behaviour of a wide class of hysteretical systems. Due to its versatility and mathematical tractability, the Bouc–Wen model has gained popularity. It has been extended and applied to a wide variety of engineering problems, including multi-degree-of-freedom (MDOF) systems, buildings, frames, bidirectional and torsional response of hysteretic systems, two- and three-dimensional continua, soil liquefaction and base isolation systems. The Bouc–Wen model, its variants and extensions have been used in structural control—in particular, in the modeling of behaviour of magneto-rheological dampers, base-isolation devices for buildings and other kinds of damping devices. It has also been used in the modelling and analysis of structures built of reinforced concrete, steel, masonry, and timber.
Tõnu Puu was an Estonian-born Swedish economist. He has been Professor of Economics at Umeå University.
Isaak D. Mayergoyz is Alford L. Ward Professor of the Department of Electrical and Computer Engineering at the University of Maryland, College Park.
The Jiles–Atherton model of magnetic hysteresis was introduced in 1984 by David Jiles and D. L. Atherton. This is one of the most popular models of magnetic hysteresis. Its main advantage is the fact that this model enables connection with physical parameters of the magnetic material. Jiles–Atherton model enables calculation of minor and major hysteresis loops. The original Jiles–Atherton model is suitable only for isotropic materials. However, an extension of this model presented by Ramesh et al. and corrected by Szewczyk enables the modeling of anisotropic magnetic materials.
References
- Ralph H. Abraham and Christopher D. Shaw. “Dynamics: A Visual Introduction.” In F. Eugene Yates, ed., Self-Organizing Systems: The Emergence of Order. New York: Plenum Press, pp. 543–597, 1987.
- Otto E. Rössler. “The Chaotic Hierarchy.” Zeitschrift für Natuforschung 1983, 38a, pp. 788–802.
- R.W. Newcomb and N. El-Leithy. “Chaos Generation Using Binary Hysteresis.” Circuits, Systems and Signal Processing September 1986, 5(3), pp. 321–341.
- L.M. Pecora and T.L. Carroll. “Synchronization in Chaotic Systems.” Physical Review Letters February 19, 1990, 64(8), pp. 821–824.
- J. Barkley Rosser, Jr. From Catastrophe to Chaos: A General Theory of Economic Discontinuities. Boston/Dordrecht: Kluwer Academic Publishers, Chapter 17, 1991.
- Clifford S. Poirot. “Financial Integration under Conditions of Chaotic Hysteresis: The Russian Financial Crisis of 1998.” Journal of Post Keynesian Economics Spring 2001, 23(3), pp. 485–508.
- J. Barkley Rosser, Jr., Marina V. Rosser, Stephen J. Guastello, and Robert W. Bond, Jr. “Chaotic Hysteresis and Systemic Economic Transformation: Soviet Investment Patterns.” Nonlinear Dynamics, Psychology, and Life Sciences October 2001, 5(4), pp. 545–566.
- Tönu Puu. Nonlinear Economic Dynamics. Berlin: Springer-Verlag, 1989.
- N. Berglund and H. Kunz. “Memory Effects and Scaling Laws in Slowly Driven Systems.” Journal of Physics A: Mathematical and General January 8, 1999, 32(1), pp. 15–39.
- Zoltán Súto and István Nagy. “Study of Chaotic and Periodic Behaviours of a Hysteresis Current Controlled Induction Motor Drive.” In Hajime Tsuboi and István Vajda, eds., Applied Electromagnetics and Computational Technology II. Amsterdam: IOS Press, pp. 233–243.
- Murano Wataru and Aiyoshi Eitaro. “Opening Door toward 21st Century. Integer Programming by the Multi-Valued Hysteresis Machines with the Chaotic Properties.” Transactions of the Institute of Electrical Engineers of Japan C 2001, 121(1), pp. 76–82.
- Hans Hauser. “Energetic Model of Ferromagnetic Hysteresis: Isotropic Magnetization.” Journal of Applied Physics September 1, 2004, 96(5), pp. 2753–2767.
- J.P. Françoise and C. Piquet. “Hysteresis Dynamics, Bursting Oscillations and Evolution to Chaotic Regimes.” Acta Biotheoretica 2005, 53(4), pp. 381–392.
- P. Vadasz. “Chaotic Dynamics and Hysteresis in Thermal Convection.” Journal of Mechanical Engineering Science “ 2006, 220(3), pp. 309-323.
- Xiangdong Liu and Chunko Xiu. “Hysteresis Modeling Based on the Hysteretic Chaotic Neural Network.” Neural Computing Applications online October 30, 2007: http://www.springerlink.com/content/x76777476785m48%5B%5D.